Алгебра логики

Математические основы ИНФОРМАТИКИ
КОНЪЮНКЦИЯ
✑ логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
⚑ Конъюнкцию также называют логическим умножением.
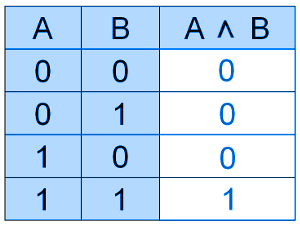
Например: A И B, A ∧ B, A * B, A & B
Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности. В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы A и B ),
ДИЗЪЮНКЦИЯ
✑ логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
⚑ Дизъюнкцию также называют логическим сложением.
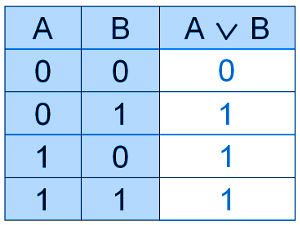
Например: A ИЛИ B; A ∨ B; A | B; A + B .
Дизъюнкция определяется следующей таблицей истинности:
ИНВЕРСИЯ
✑ логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
⚑ Инверсию также называют логическим отрицанием.
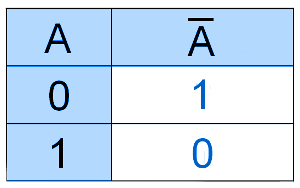
Например: НЕ А; ¬А; А− .
Инверсия определяется следующей таблицей истинности.
ИМПЛИКАЦИЯ
✑ Сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием (A), а второе (A) является следствием условия (A).
.
⚑ Импликацию также называют логическим следованием.
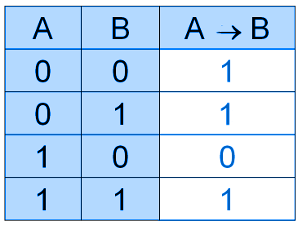
Свойства импликации: A → B = ¬ A ∨ B.
Импликация A→B ложна, если A=1 и B=0. Если A=0, то импликация A→B истинна при любом значении B, (из лжи может следовать истинна).
ЭКВИВАЛЕНТНОСТЬ
✑ сложное логическое выражение, которое истинно на равных значениях переменных A и B
.
⚑ Эквивалентность также называют логической равнозначностью.
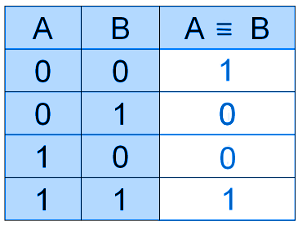
Для записи эквивалентности используют следующие знаки: ↔, ⇔.
Свойства эквивалентности:
- Эквивалентность истинна на равных наборах значений переменных A и B.
- КНФ
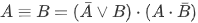
- ДНФ
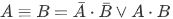
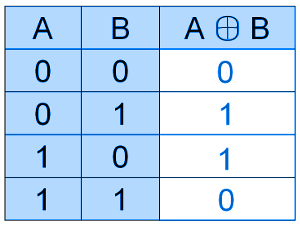
СТРОГАЯ ДИЗЪЮНКЦИЯ/исключающее ИЛИ
✑ Строгая дизъюнкция истинна, если значения аргументов не равны.
.
⚑ Сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
СТРЕЛКА ПИРСА
✑ Бинарная логическая операция, булева функция над двумя переменными.
.
⚑ Названа в честь Чарльза Пирса и введена в алгебру логики в 1880-1881гг.
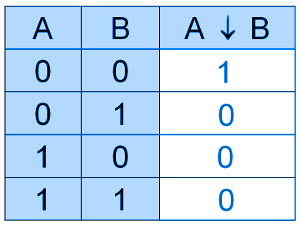
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
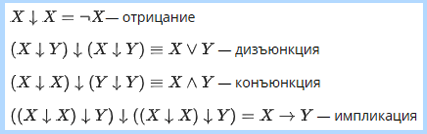
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR)
ШТРИХ ШИФФЕРА
✑ Булева функция двух переменных или бинарная логическая операция.
.
⚑ Введена в рассмотрение Генри Шеффером в 1913 г.
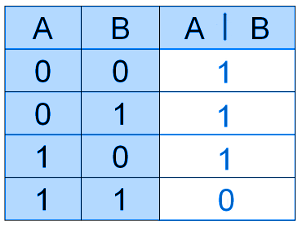

Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении:
- Действие в скобках (если они есть)
- Инверсия(отрицание);
- Конъюнкция (логическое умножение);
- Дизъюнкция и строгая дизъюнкция (логическое сложение);
- Импликация (следствие);
- Эквивалентность (тождество).
Свойства логических операций:

Логические переменные и логические функции:


