
В задание №19_20_21
Тема: Теория игр. Поиск выигрышной стратегии.
Проверяется умение анализировать алгоритм логической игры. Умение найти выигрышную стратегию игры. Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию.
Немного теории:
☆ Все позиции в простых играх делятся на выигрышные и проигрышные
- выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
- если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
- выигрышные и проигрышные позиции можно охарактеризовать так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
- позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
Одна куча:
Задание 19
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в кучу один камень или
- Добавить в кучу три камня или
- Увеличить количество камней в куче в четыре раза.
Например, имея кучу из 20 камней, за одни ход можно получить кучу из 21, 23 или 80 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 78. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 78 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 77.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Вася выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:

Ответ: 5
Задание 20
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Теперь попробуем определить значение S, при которых у Пети будет выигрышная стратегия, причём Петя не сможет выиграть первым ходом, но сможет выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.

Ответ: 16 18
Задание 21
- У Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
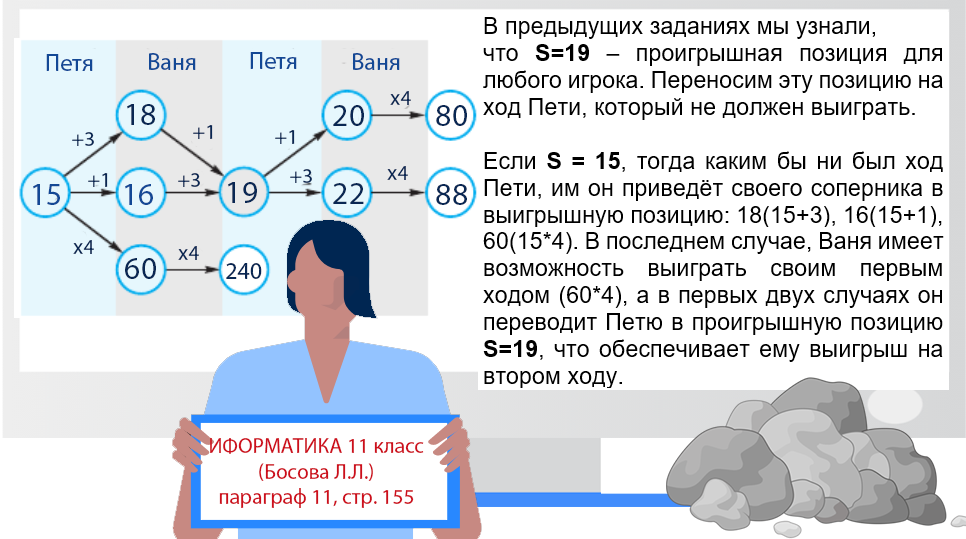
Ответ: 15
ОДНА КУЧА НА УВЕЛИЧЕНИЕ
Задание 19 пишем программу на Phyton
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в кучу один камень или
- Добавить в кучу два камня или
- Увеличить количество камней в куче в четыре раза.
Например, имея кучу из 20 камней, за одни ход можно получить кучу из 21, 22 или 79 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 85. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 85 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 84.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
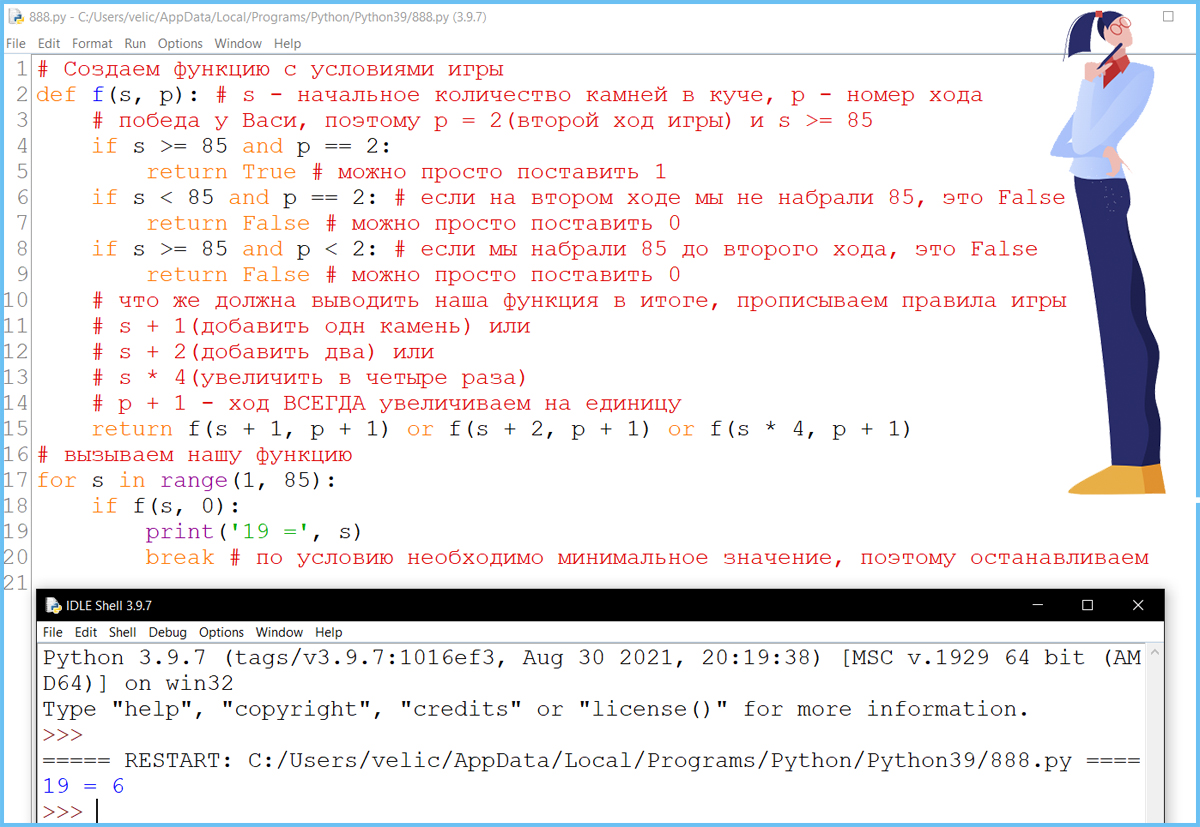
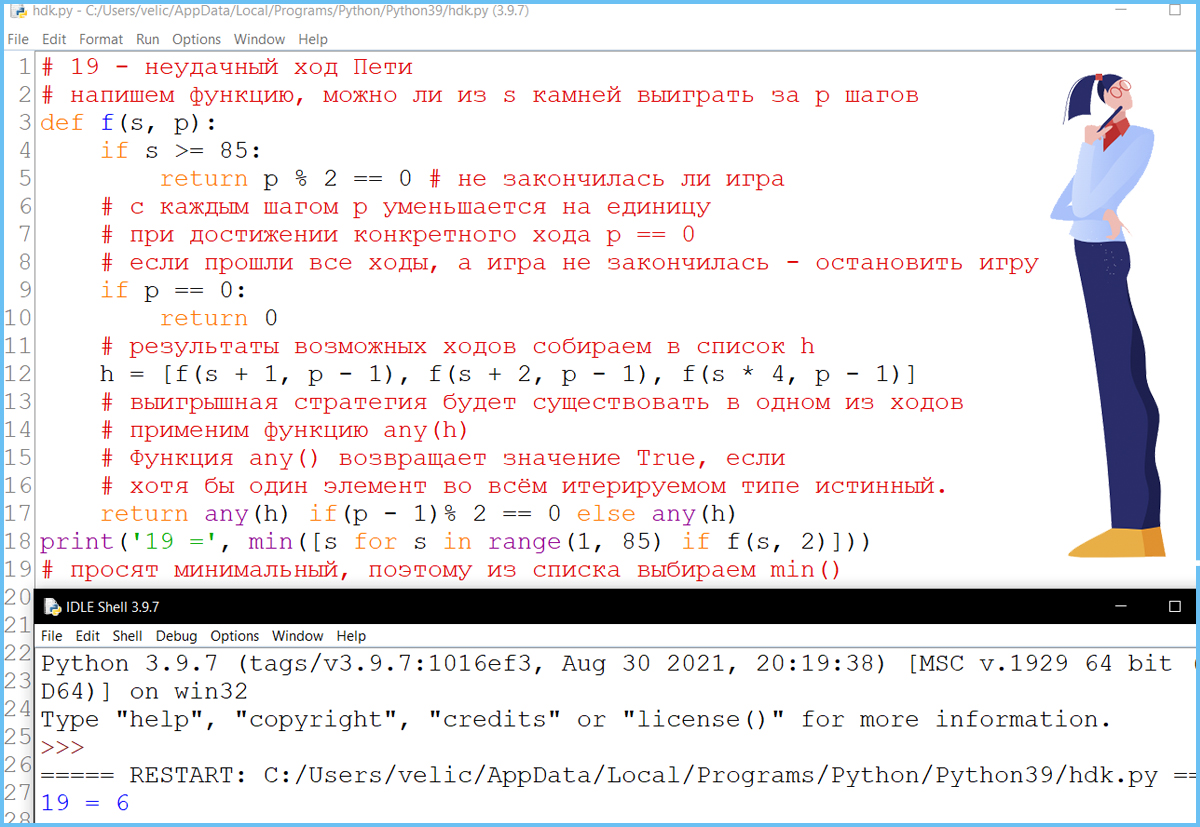
Известно, что Ваcя выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 19 - вариант I - Phyton
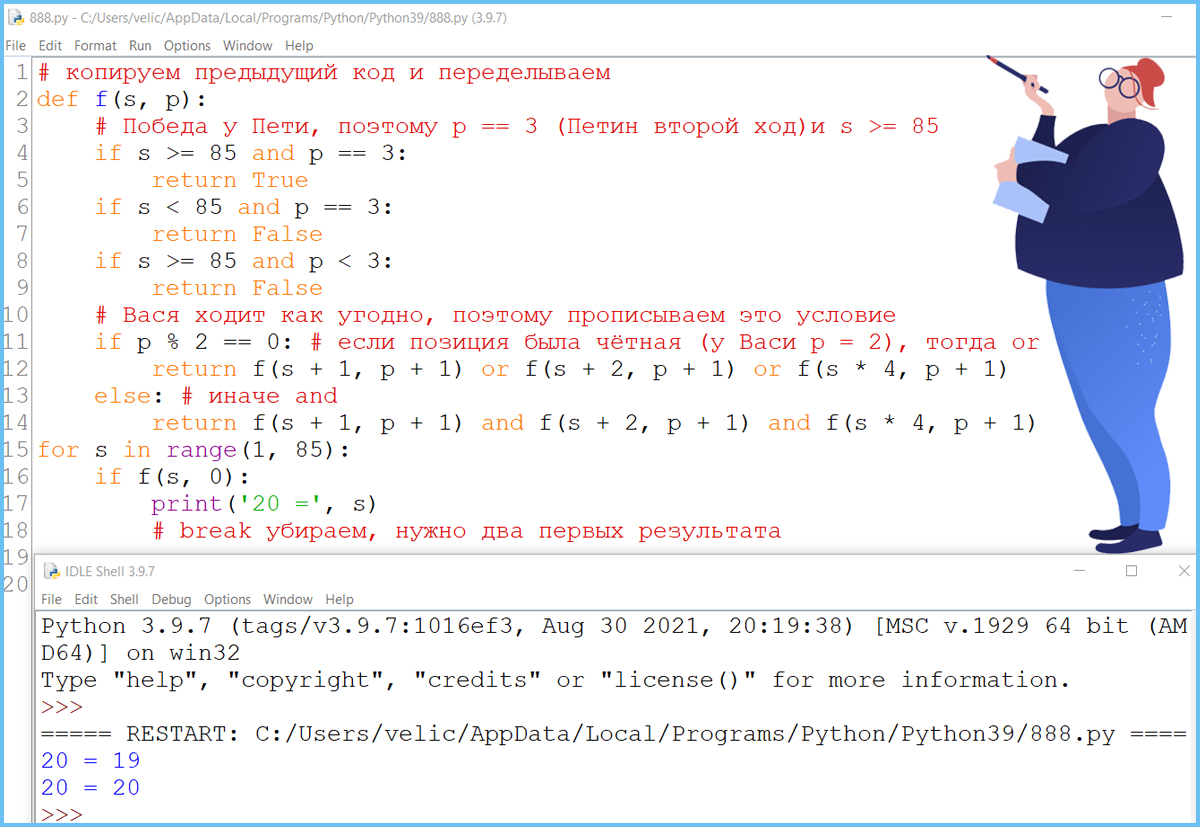
Задание 20 - вариант I - Phyton
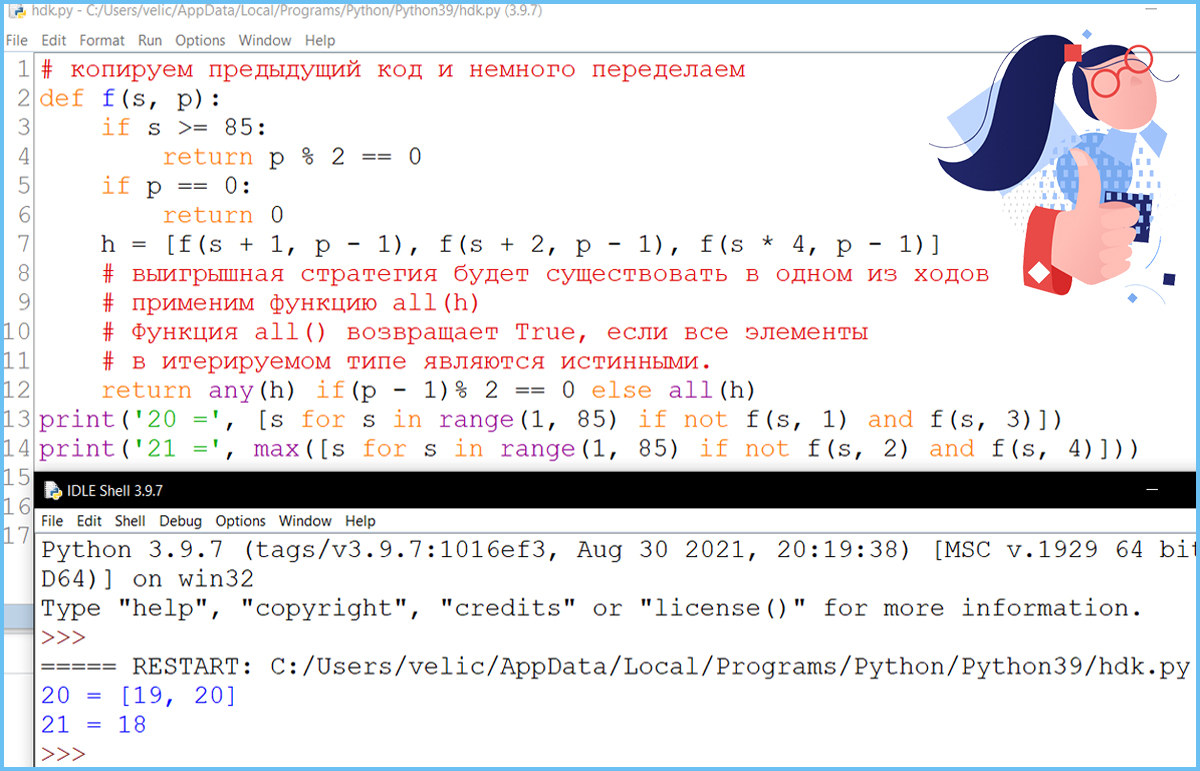
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваcя.
Найденные значения запишите в ответе в порядке возрастания.
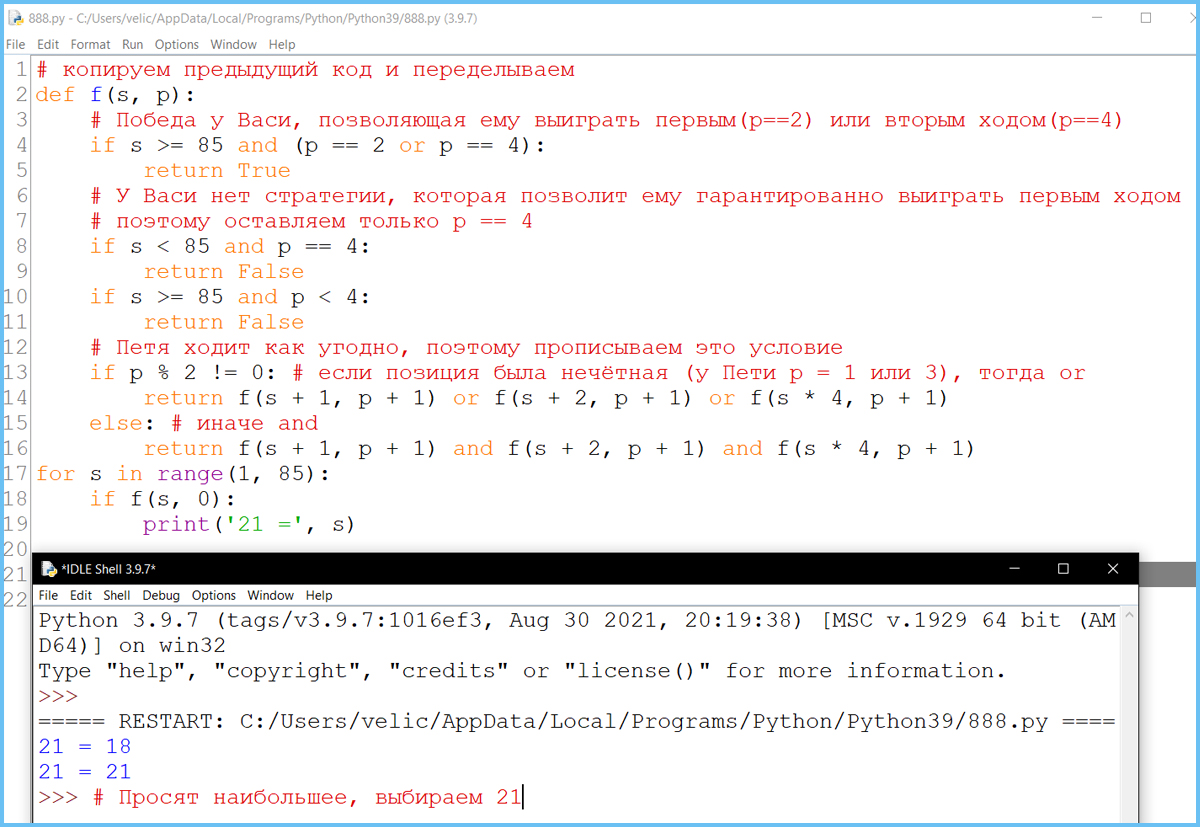
Задание 21 - вариант I - Phyton
Для игры, описанной в задании 19, найдите максимальное значение S, при котором одновременно выполняются два условия:
- У Ваcи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Ваcи нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Задание 19 - вариант II - Phyton
Задание 20-21 - вариант II - Phyton
ОДНА КУЧА НА УМЕНЬШЕНИЕ
Задание 19_20_22 пишем программу на Phyton
Например, из кучи из 19 камней можно получить кучу из 14 камней или кучу из 6 камней. Игра завершается в тот момент, когда из кучи убирается последний камень. Победителем считается игрок, сделавший последний ход, т. е. убравший из кучи последний камень.
В начальный момент в куче было S камней; S > 0.
Ответьте на следующие вопросы:
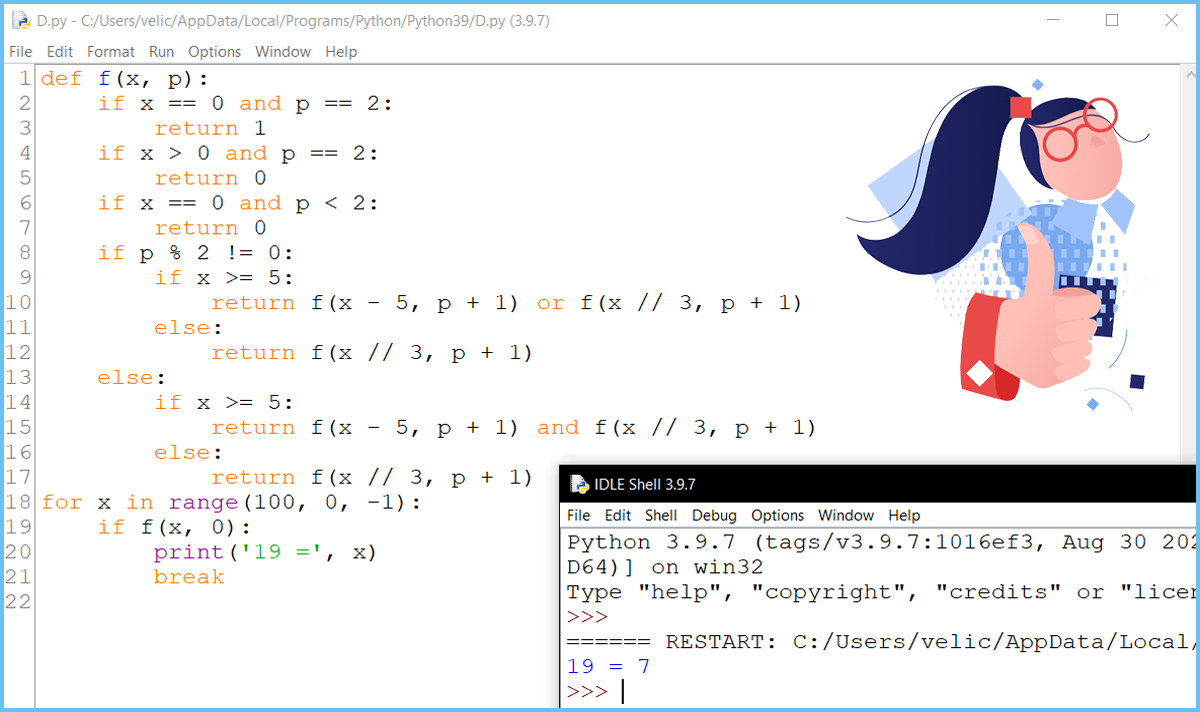
Вопрос 1. Укажите максимальное значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Вопрос 2. Найдите наименьшее и наибольшее значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Вопрос 3. Найдите максимальное значение S, при котором одновременно выполняются два условия:
- у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом;
- Петя может выбирать, каким ходом выиграет Ваня.
Задание 19 - 21 - вариант I - Phyton
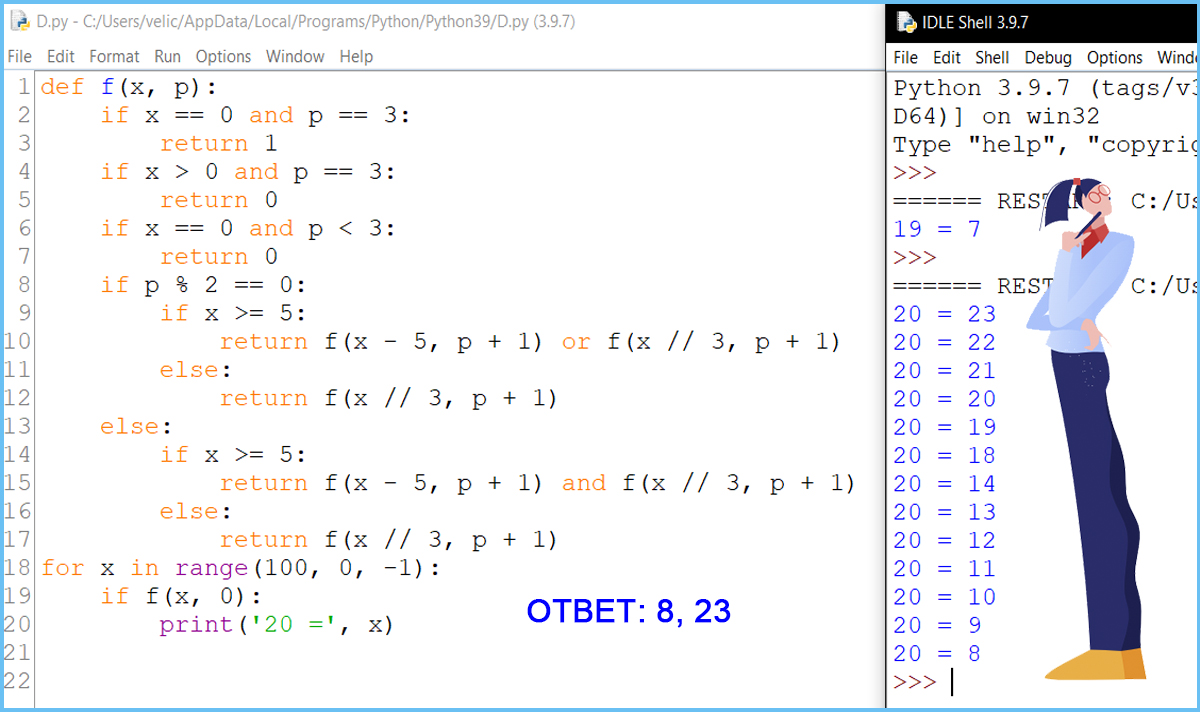
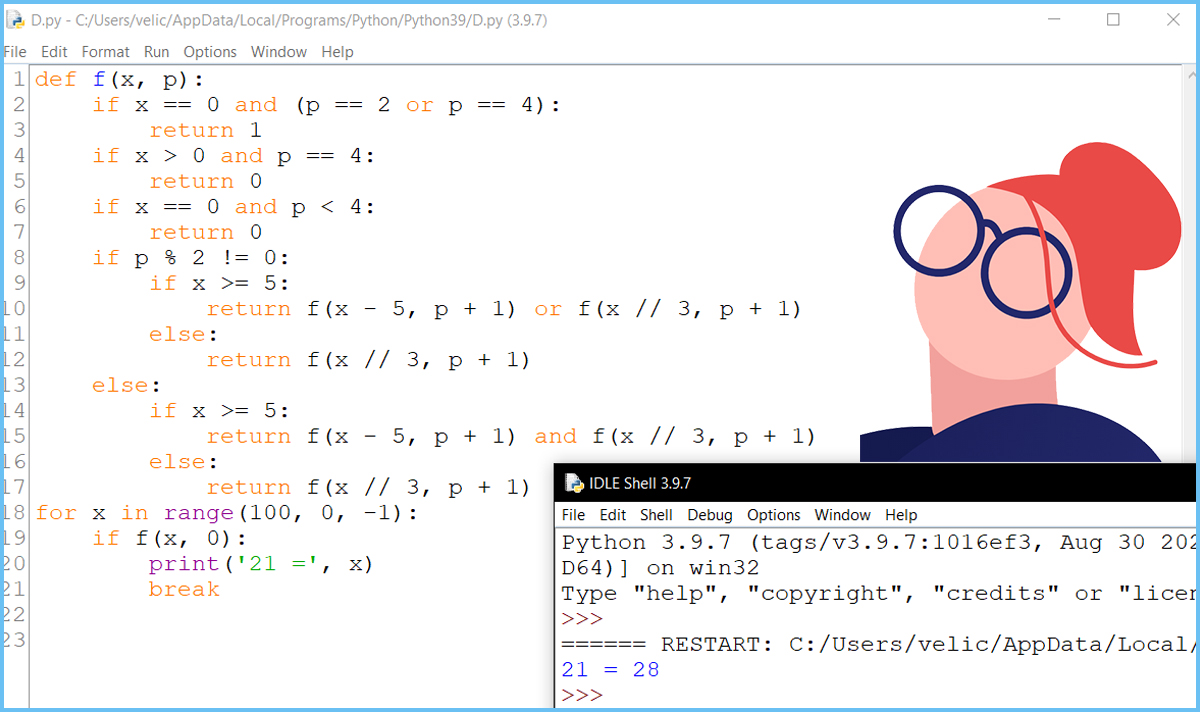
Задание 19 - 21 - вариант II - Phyton
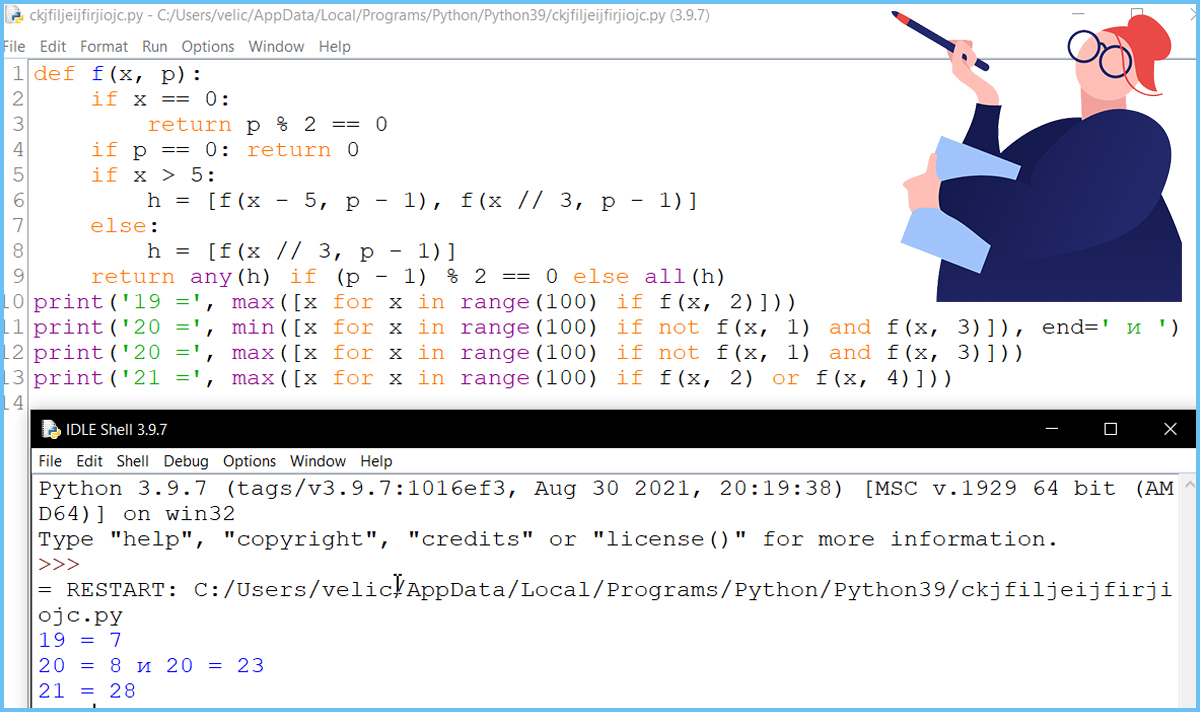
Задание 19_20_22 (Поляков) пишем программу Phyton
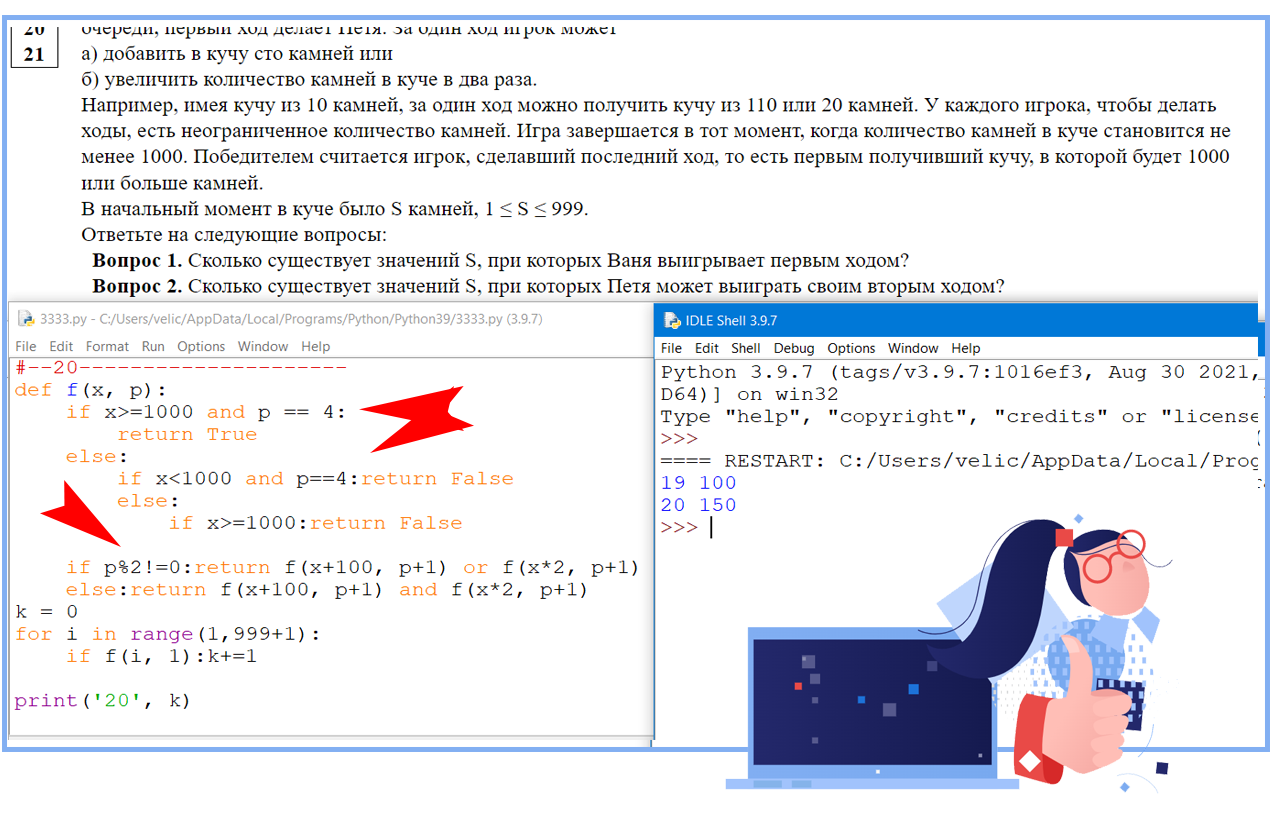
- добавить в кучу сто камней или
- увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда количество камней в куче становится не менее 1000. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 1000 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 999.
Ответьте на следующие вопросы:
Вопрос 1. Сколько существует значений S, при которых Ваня выигрывает первым ходом?
Вопрос 2. Сколько существует значений S, при которых Петя может выиграть своим вторым ходом?
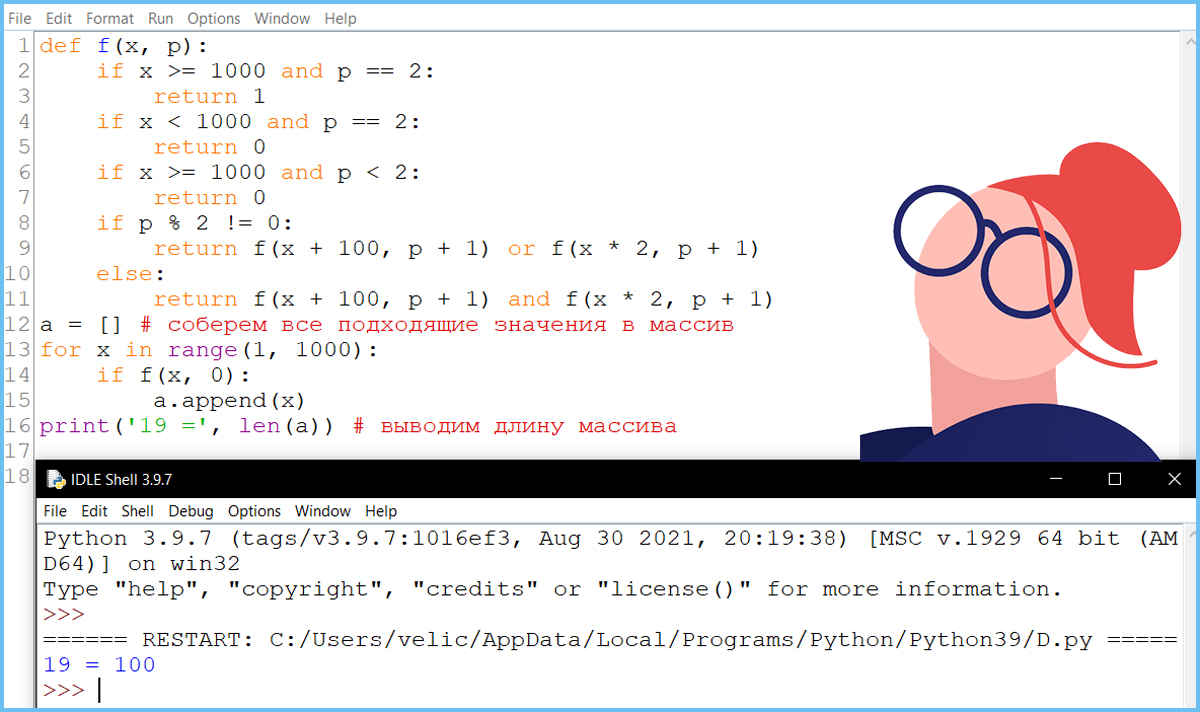
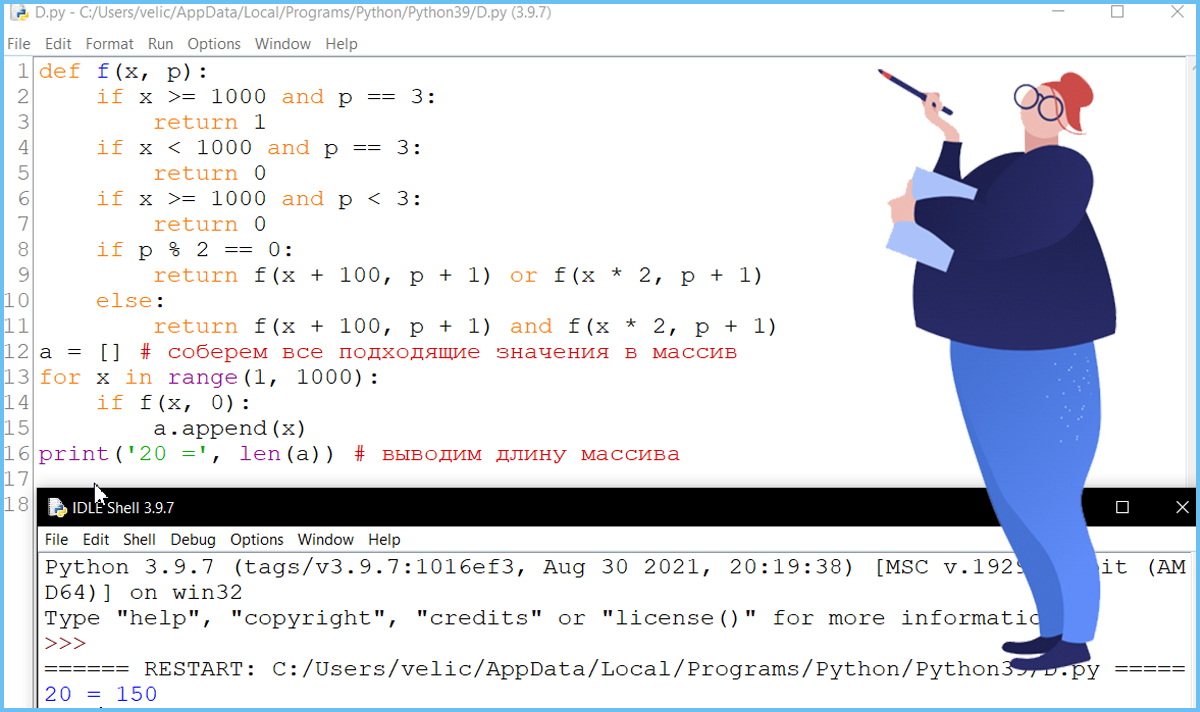
Задание 19 - вариант I - Phyton
Две кучи - варианты решений
Задание 19 (разбираем задание)
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в одну из куч (по своему выбору) один камень или
- Добавить в одну из куч (по своему выбору) удвоенное число камне из другой кучи.
Например, пусть в одной куче 8 камней, а в другой куче 5 камней. Тогда за один ход можем получить четыре позиции: (9, 5); (18, 5); (8, 6); (8, 21).
Для того что бы играть, у игроков есть неограниченное количество камне.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было 9 камней, во второй S камней: 1 ≤ S ≤ 67.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Вася выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
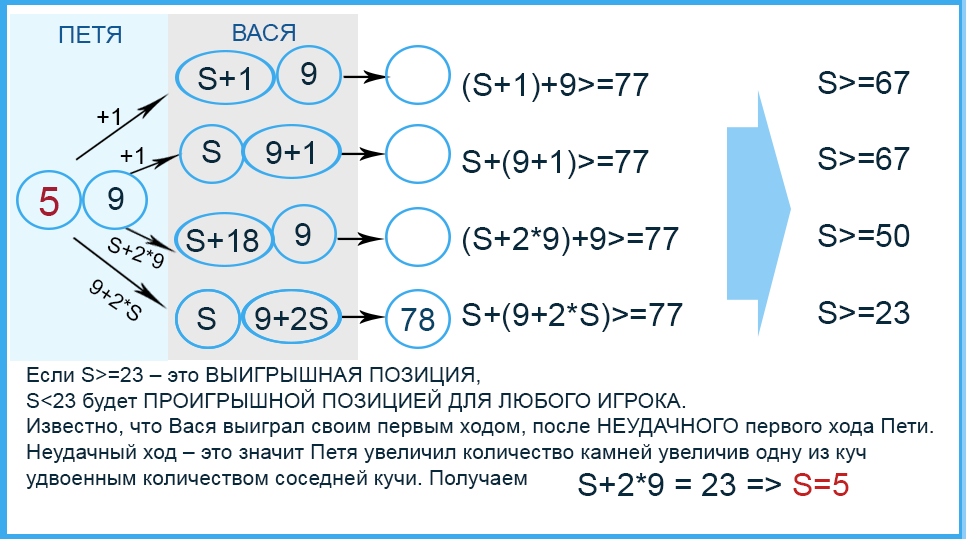
Можно решить с помощью рассуждений:
- Если S = 67, то добавив в любую кучу один камень (67+1+9=77), или добавить удвоенную соседнюю кучу в любую из куч (9+(67+2*9)=94 или ((9+2*67)+67=210), Петя становится победителем.
- Если S = 66, добавив удвоенную соседнюю кучу в любую из куч (9+(66+2*9)=93 или ((9+2*66)+66=207), Петя становится победителем.
- Если S = 65, добавив удвоенную соседнюю кучу в любую из куч (9+(65+2*9)=92 или ((9+2*65)+65=204), Петя становится победителем.
- Обратим внимание, если удваиваем 9 камней и добавляем во вторую кучу, уменьшение ровно на 1, поэтому ускорим процесс 92-77=15, 65 -15 =50, идем дальше
- Если S = 50, добавив удвоенную соседнюю кучу в любую из куч (9+(50+2*9)=77 или ((9+2*50)+50=159), Петя становится победителем.
- У нас остается только один вариант, ускорим процес, усли удваиваем вторую кучу, уменьшение ровно на три, поэтому ускорим процесс 159-77=82, 82/3=27,333, 50-27=23
- Если S = 23, добавив удвоенную соседнюю кучу в эту из куч ((9+2*23)+23=78), Петя становится победителем. СТОП!!!
Можно проверить программой:
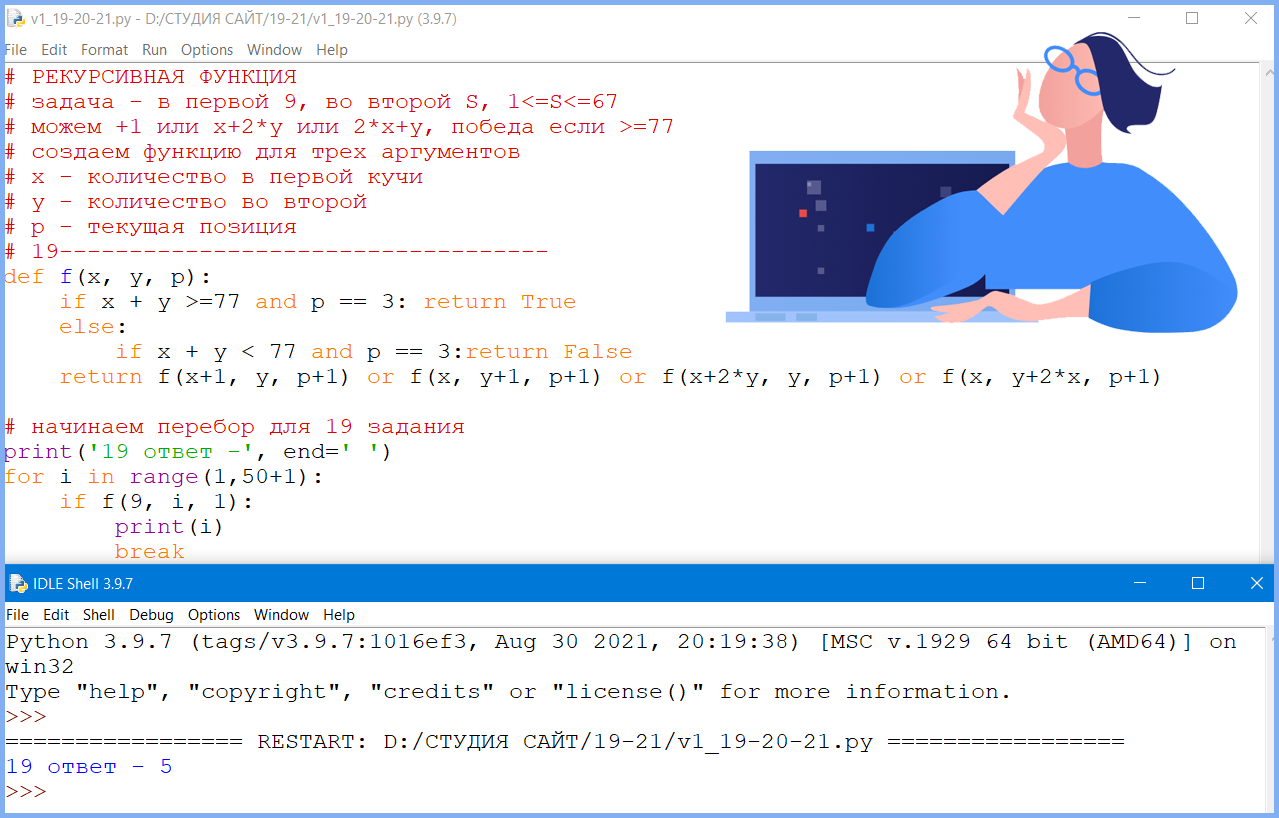
# 19-----------------------------------
def f(x, y, p):
if x + y >=77 and p == 3: return True
else:
if x + y < 77 and p == 3:return False
return f(x+1, y, p+1) or f(x, y+1, p+1) or f(x+2*y, y, p+1) or f(x, y+2*x, p+1)
# начинаем перебор для 19 задания
print('19 ответ -', end=' ')
for i in range(1,50+1):
if f(9, i, 1):
print(i)
break Ответ: 5
Задание 20 (разбираем задание)
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
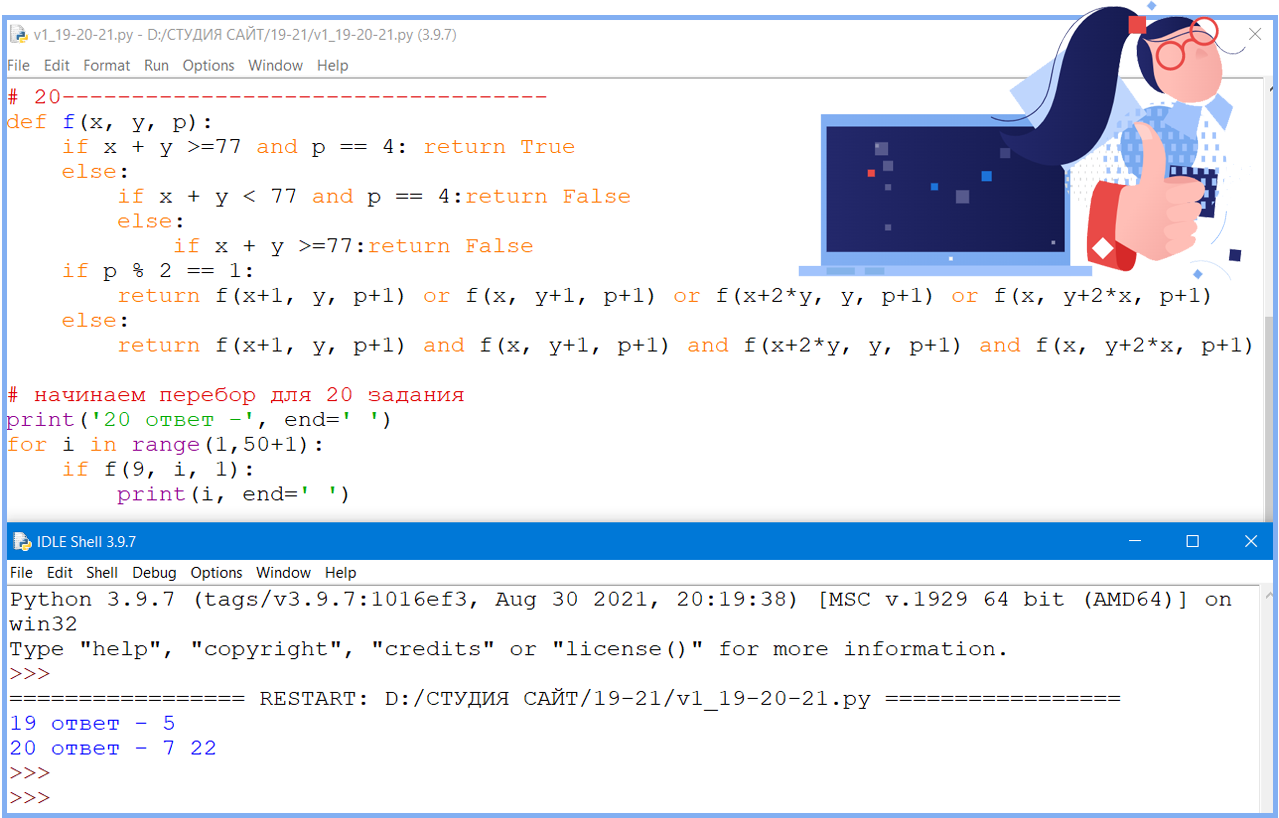
Ответ: 7 22
Задание 21 (разбираем задание)
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
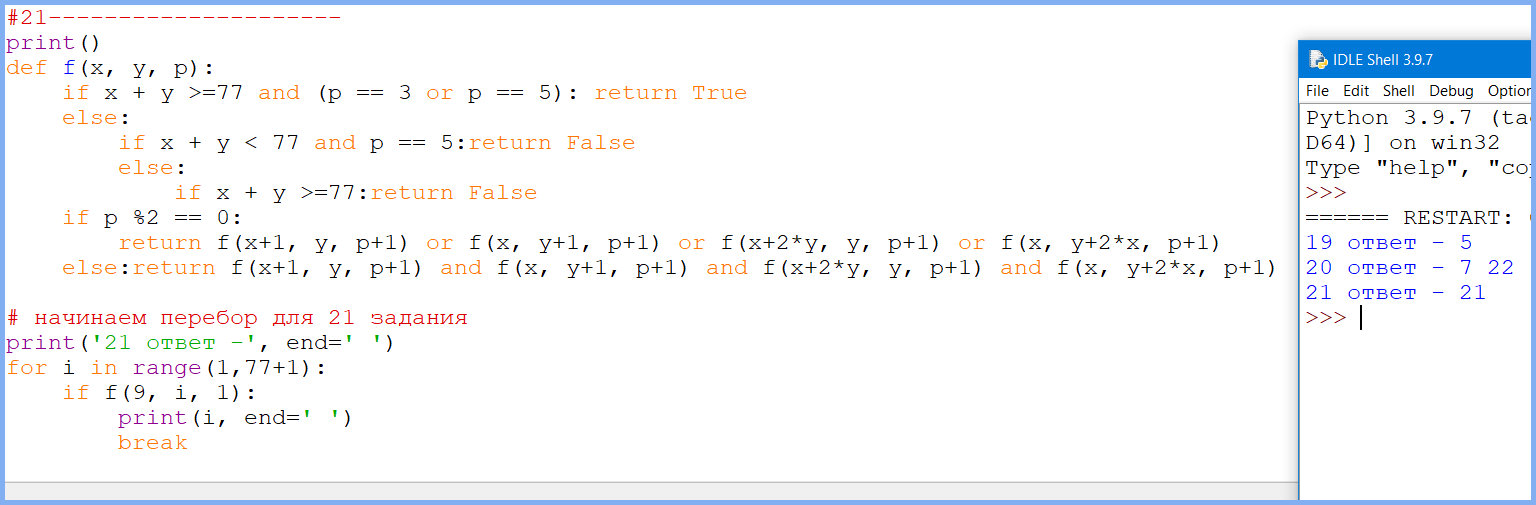
Ответ: 21
Три кучи - варианты решений
Задание 19_20_21 (разбираем задание)
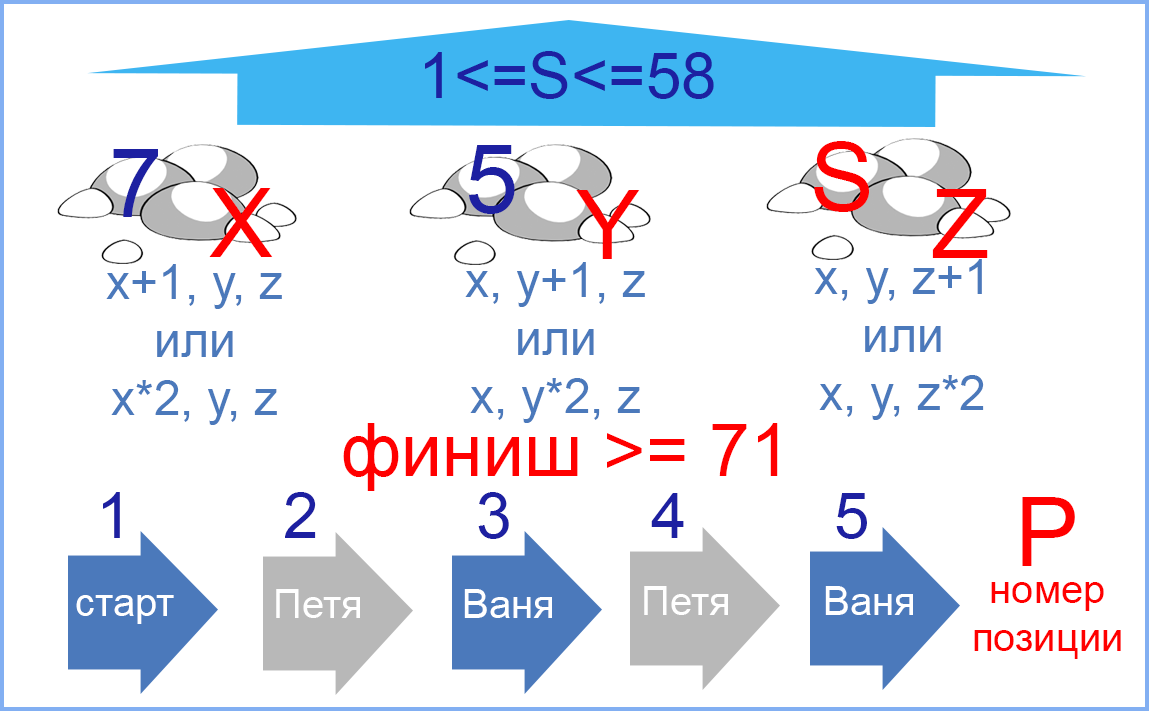
(№ 4725) (И. Осипов) Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат три кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) три камня или увеличить количество камней в куче в два раза. Например, пусть в первой куче 10 камней, во второй 7, а в третьей 4 камня; такую позицию в игре будем обозначать (10, 7, 4). Тогда за один ход можно получить любую из шести позиций: (13, 7, 4), (20, 7, 4), (10, 10, 4), (10, 14, 4), (10, 7, 7), (10, 7, 8). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 71. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, что в кучах всего будет 71 или больше камней. В начальный момент в первой куче было семь камней, во второй куче пять камней, в третьей куче – S камней; 1 ≤ S ≤ 58.
Ответьте на следующие вопросы:
Вопрос 1.При некотором значении S Ваня одержал победу свои первым ходом после неудачного хода Пети. Укажите минимальное значение S, при котором это возможно.
Вопрос 2. Найдите минимальное и максимальное значения S, при которых Петя выигрывает вторым ходом при любом ходе Вани.
Вопрос 3. Найдите значение S, при котором одновременно выполняются два условия: а) у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; б) у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
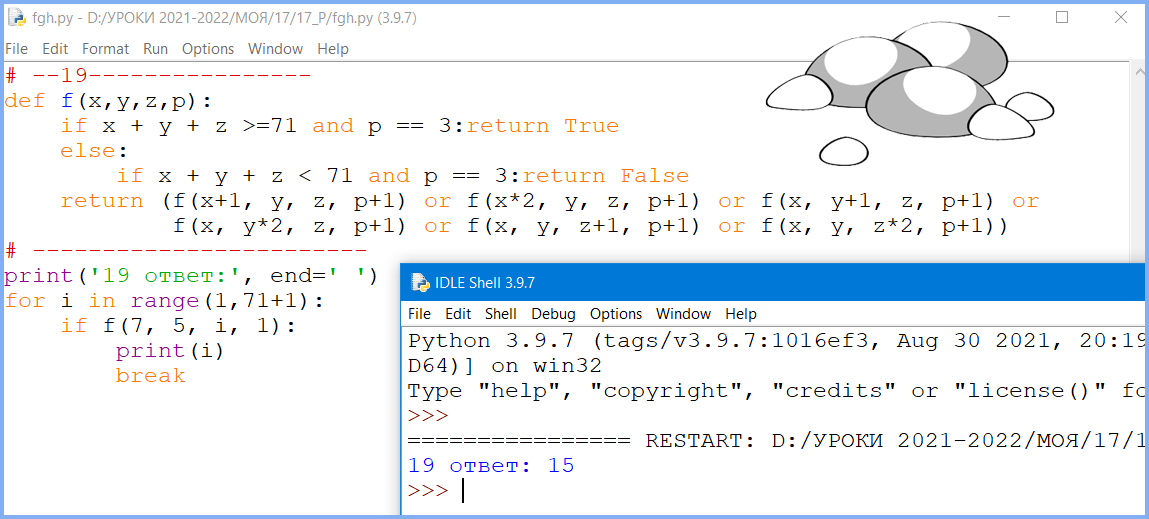
# --19----------------
def f(x,y,z,p):
if x + y + z >=71 and p == 3:return True
else:
if x + y + z < 71 and p == 3:return False
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
# ------------------------
print('19 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i)
break Ответ: 15
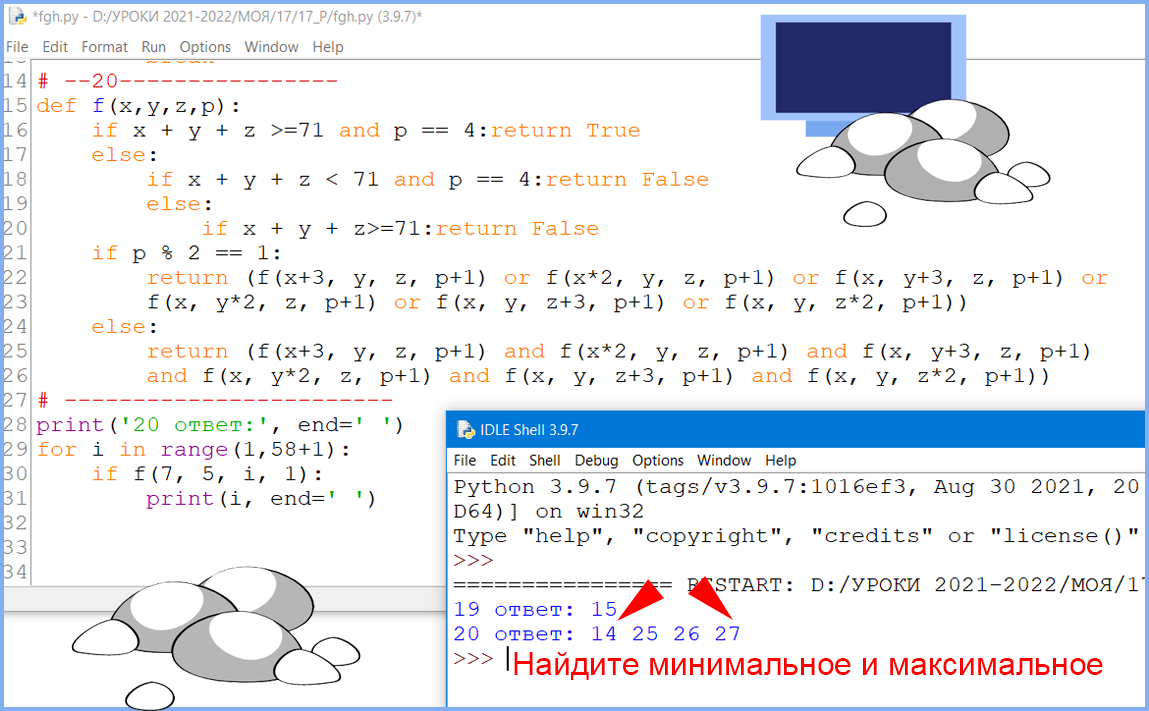
# --20----------------
def f(x,y,z,p):
if x + y + z >=71 and p == 4:return True
else:
if x + y + z < 71 and p == 4:return False
else:
if x + y + z>=71:return False
if p % 2 == 1:
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
else:
return (f(x+3, y, z, p+1) and f(x*2, y, z, p+1) and f(x, y+3, z, p+1)
and f(x, y*2, z, p+1) and f(x, y, z+3, p+1) and f(x, y, z*2, p+1))
# ------------------------
print('20 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i, end=' ') Ответ: 14 27
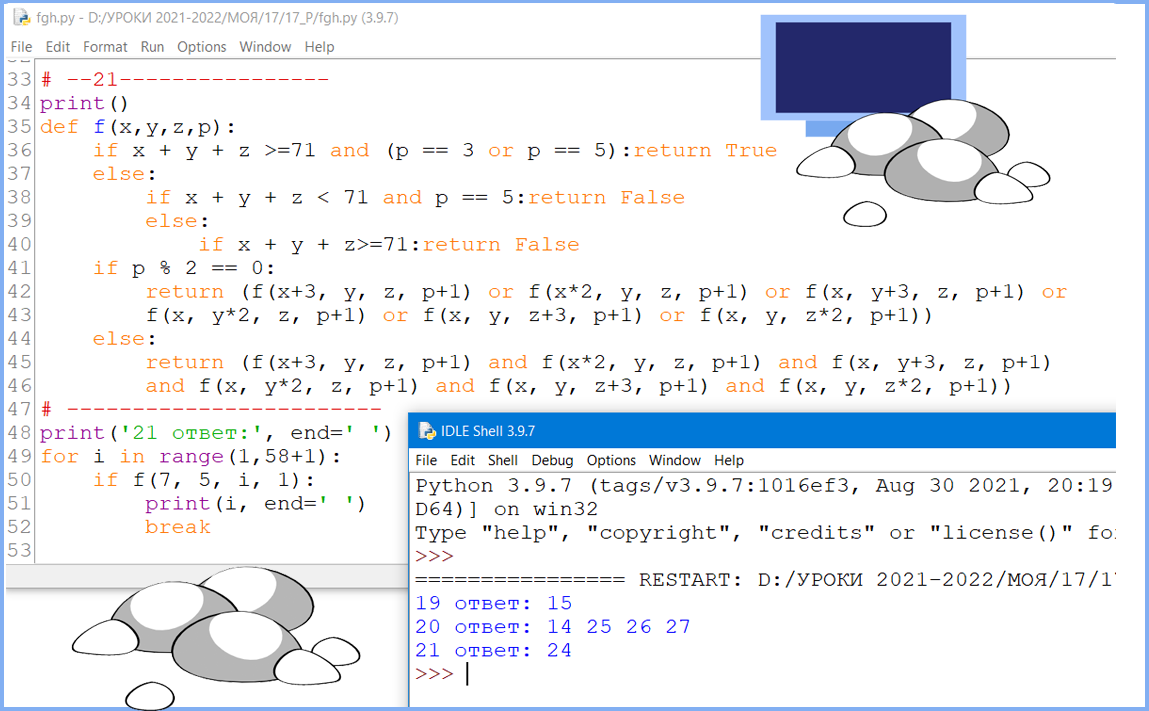
# --21----------------
print()
def f(x,y,z,p):
if x + y + z >=71 and (p == 3 or p == 5):return True
else:
if x + y + z < 71 and p == 5:return False
else:
if x + y + z>=71:return False
if p % 2 == 0:
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
else:
return (f(x+3, y, z, p+1) and f(x*2, y, z, p+1) and f(x, y+3, z, p+1)
and f(x, y*2, z, p+1) and f(x, y, z+3, p+1) and f(x, y, z*2, p+1))
# ------------------------
print('21 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i, end=' ')
break Ответ: 24

