
ЕГЭ 2022 сборник Крылова С.С.
Задание 8. Перебор слов и системы счисления
Вариант 1
Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых ровно две цифры 4, и при этом никакая нечётная цифра не стоит рядом с цифрой 4.
Решение:
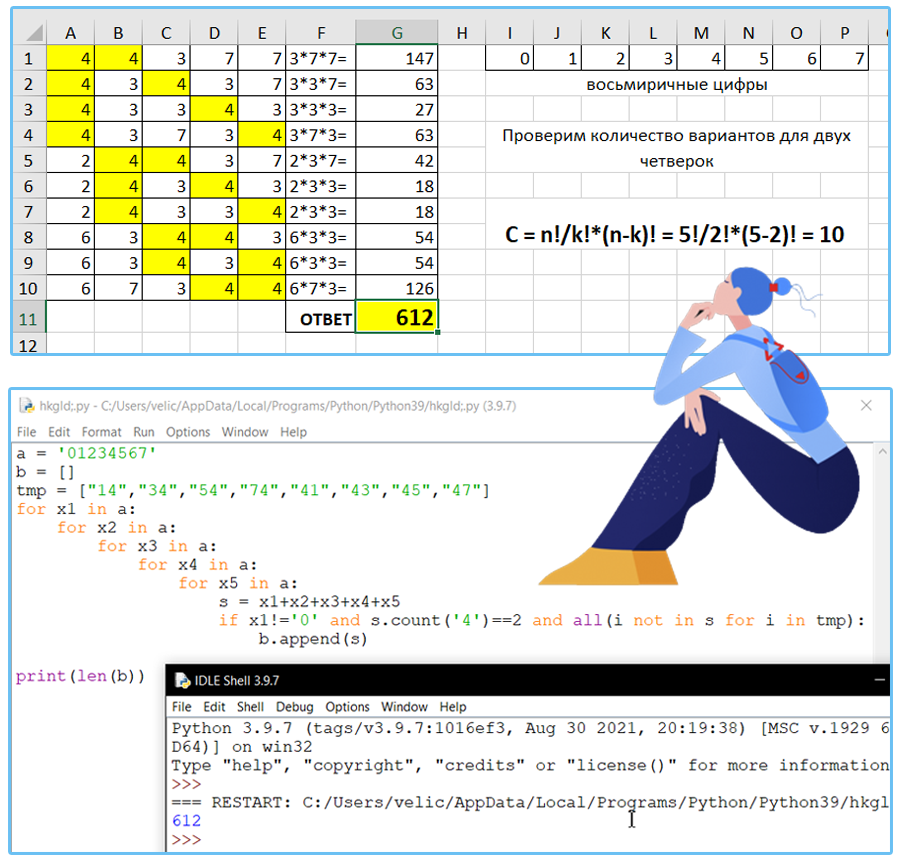
Ответ: 612
Вариант 2
Определите количество пятизначных чисел, записанных в четверичной системе счисления, в записи которых ровно одна цифра 3, и при этом цифра 0 не стоит рядом с цифрой 3.
Решение:
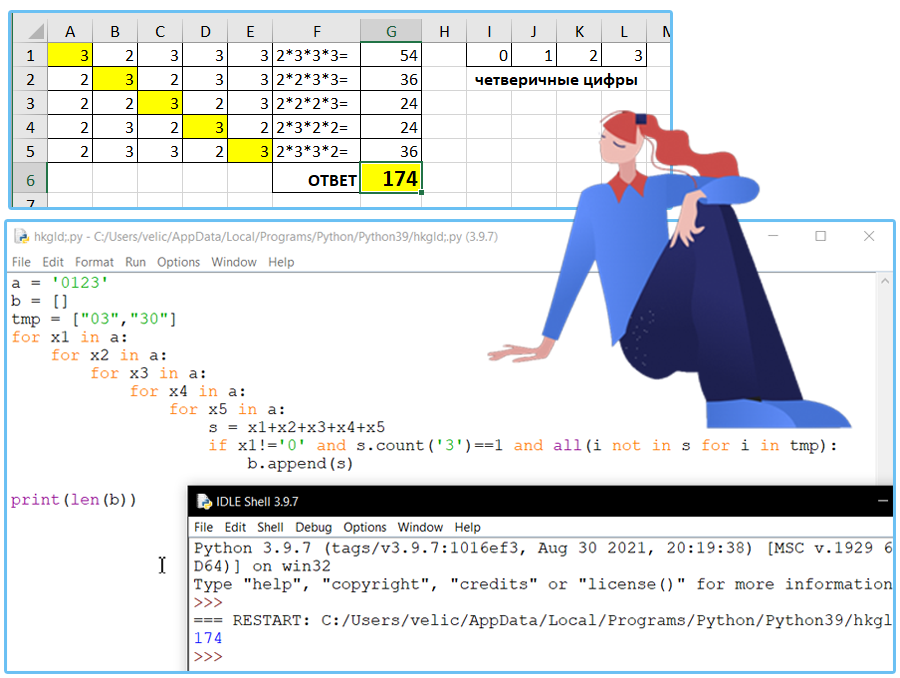
Ответ: 174
Вариант 3
Все шестибуквенные слова, в составе которых могут быть только русские буквы С, О, Р, Н, Я, К, записаны в алфавитном порядке и пронумерованы начиная с 1.
Ниже приведено начало списка:
- КККККК
- КККККН
- КККККО
- КККККР
- КККККС
- КККККЯ
- ККККНК
…..
Под каким номером в списке идёт первое слово, которое содержит не более трёх букв К и ровно две буквы Я?
Решение:
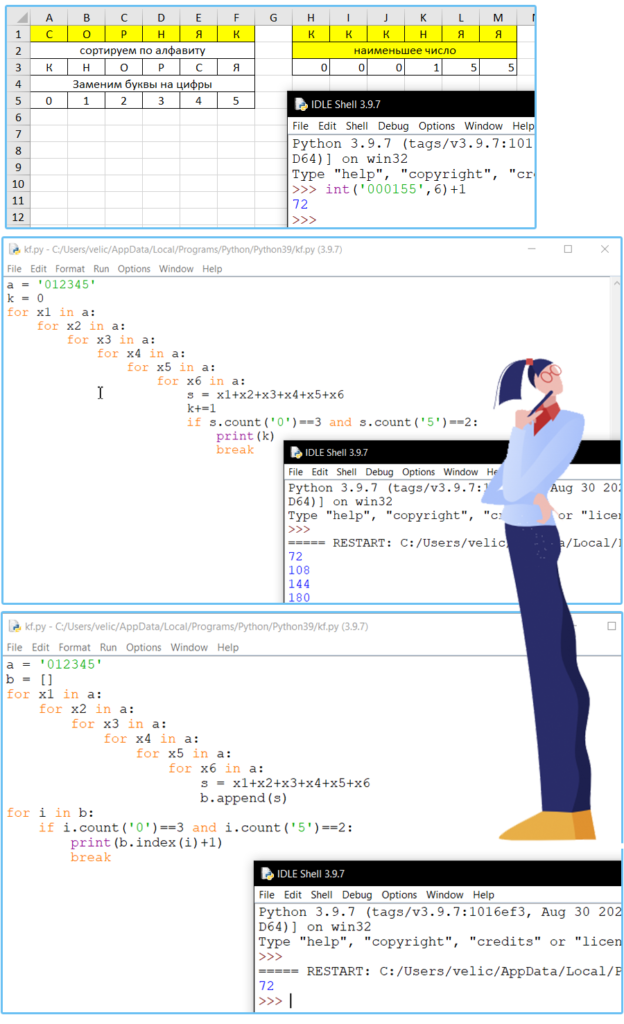
Ответ: 72
Вариант 4
Все шестибуквенные слова, в составе которых могут быть только русские буквы П, О, Л, Ь, З, А, записаны в алфавитном порядке и пронумерованы начиная с 1.
Ниже приведено начало списка:
- АААААА
- АААААЗ
- АААААЛ
- АААААО
- АААААП
- АААААЬ
- ААААЗА
…..
Под каким номером в списке идёт первое слово, которое содержит не более одной букв Ь, ровно одну букву А и не более двух букв З?
Решение:
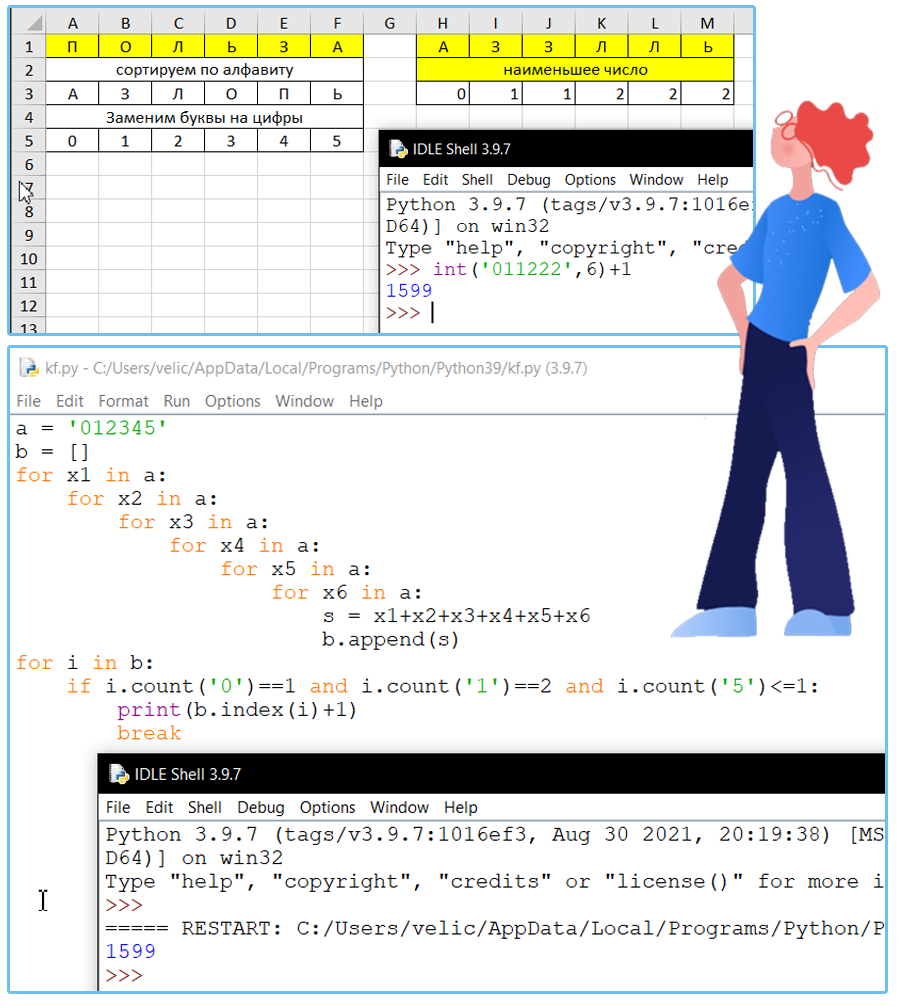
Ответ: 1599
Вариант 5
Все 4-буквенные слова, в составе которых могут быть только русские буквы А, Т, О, М, записаны в алфавитном порядке и пронумерованы начиная с 1.
Ниже приведено начало списка:
- АААА
- АААМ
- АААО
- АААТ
- ААМА
- ААММ
…..
Под каким номером в списке идёт первое слово, которое начинается с буквы О?
Решение:
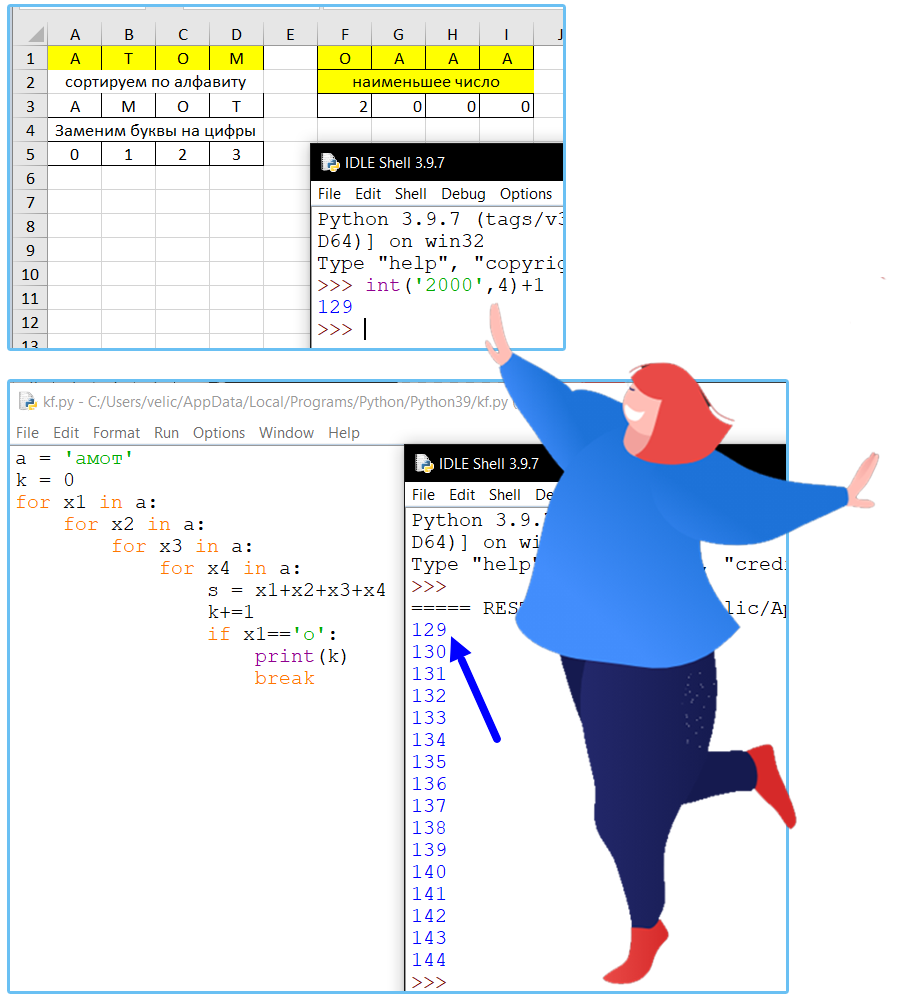
Ответ: 129
Вариант 6
Все 4-буквенные слова, в составе которых могут быть только русские буквы П, Р, А, В, О, записаны в алфавитном порядке и пронумерованы начиная с 1.
Ниже приведено начало списка:
- АААА
- АААВ
- АААО
- АААП
- АААР
- ААВА
- ААВВ
…..
Под каким номером в списке идёт первое слово, которое начинается с буквы П?
Решение:
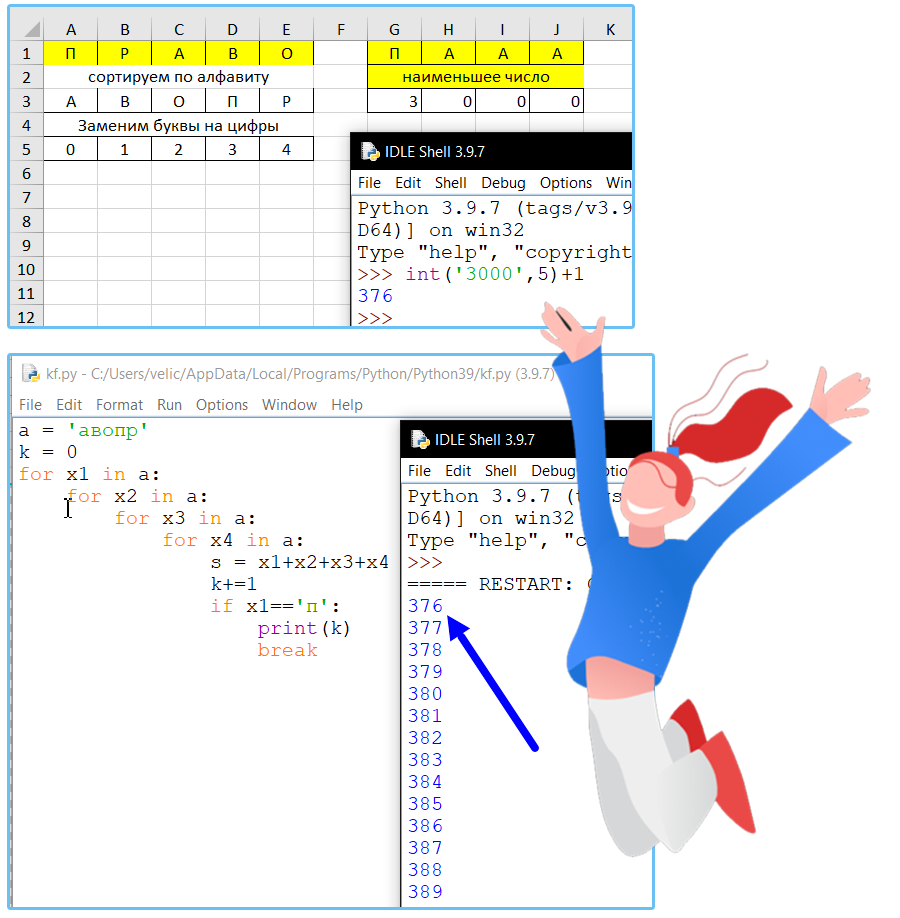
Ответ: 376
Вариант 7
Все пятибуквенные слова, в составе которых могут быть только русские буквы М, А, С, Л, О, записаны в алфавитном порядке и пронумерованы начиная с 1.
Ниже приведено начало списка:
- ААААА
- ААААЛ
- ААААМ
- ААААО
- ААААС
- АААЛА
…..
Под каким номером в списке идёт первое слово, которое содержит не более одной буквы А, ровно две буквы М, не содержит ни одной буквы Л?
Решение:
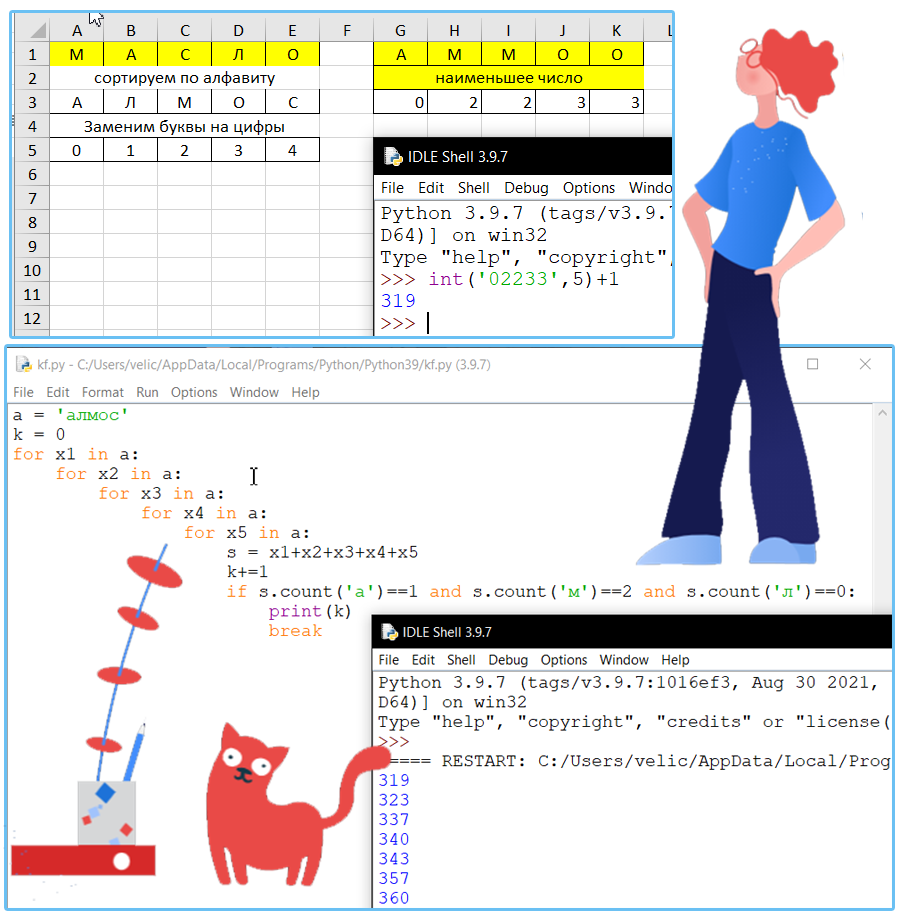
Ответ: 319
Вариант 8
Все шестибуквенные слова, в составе которых могут быть только русские буквы В, А, Л, И, К, записаны в алфавитном порядке и пронумерованы начиная с 1.
Ниже приведено начало списка:
- АААААА
- АААААВ
- АААААИ
- АААААК
- АААААЛ
- ААААВА
…..
Под каким номером в списке идёт первое слово, которое содержит не более двух букв А, ровно две буквы В, не содержит ни одной буквы И?
Решение:
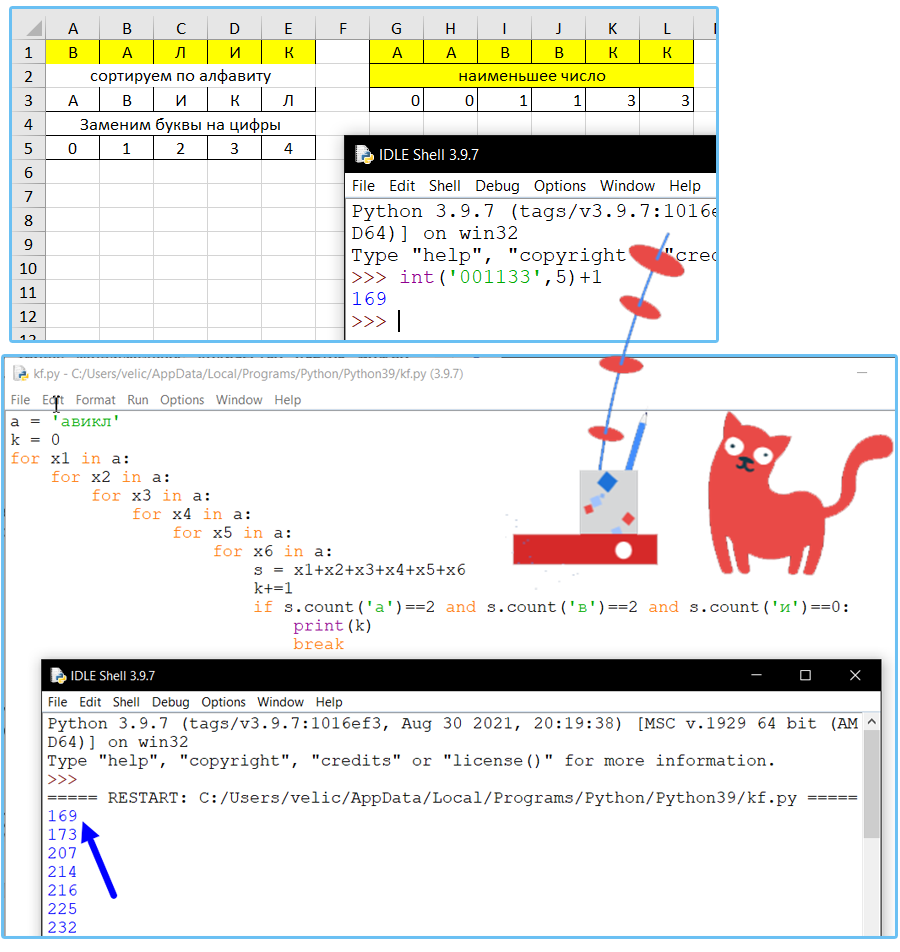
Ответ: 169
Вариант 9
Сколько существует различных трёхзначных чисел, записанных в четверичной системе счисления, в записи которых цифры следуют слева направо в строго убывающем порядке?
Решение:
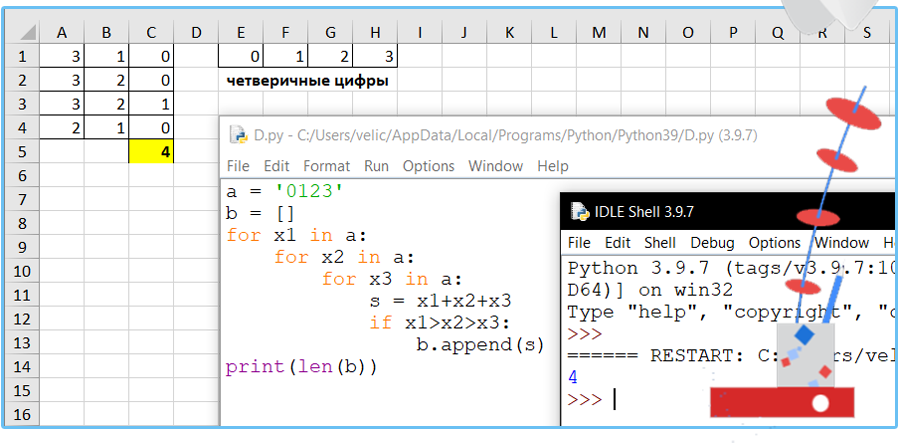
Ответ: 4
Вариант 10
Сколько существует различных трёхзначных чисел, записанных в пятеричной системе счисления, в записи которых цифры следуют слева направо в строго убывающем порядке?
Решение:
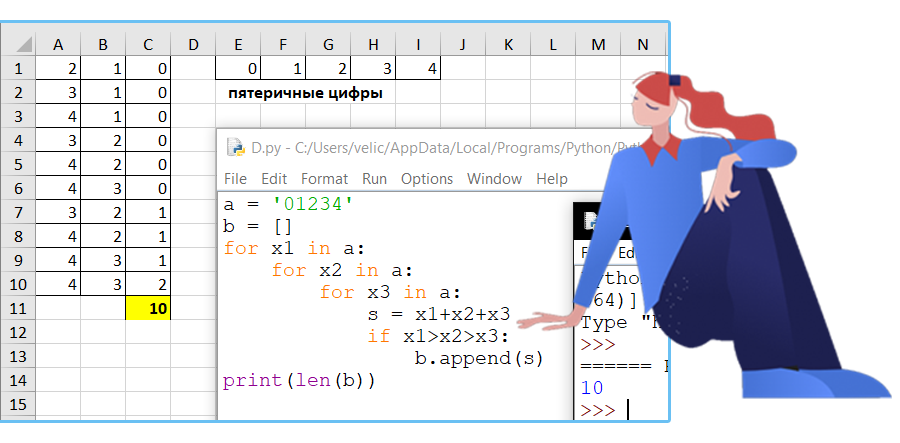
Ответ: 10
Вариант 11
Сколько существует различных трёхзначных чисел, записанных в четверичной системе счисления, в записи которых цифры следуют слева направо в невозрастающем порядке?
Решение:
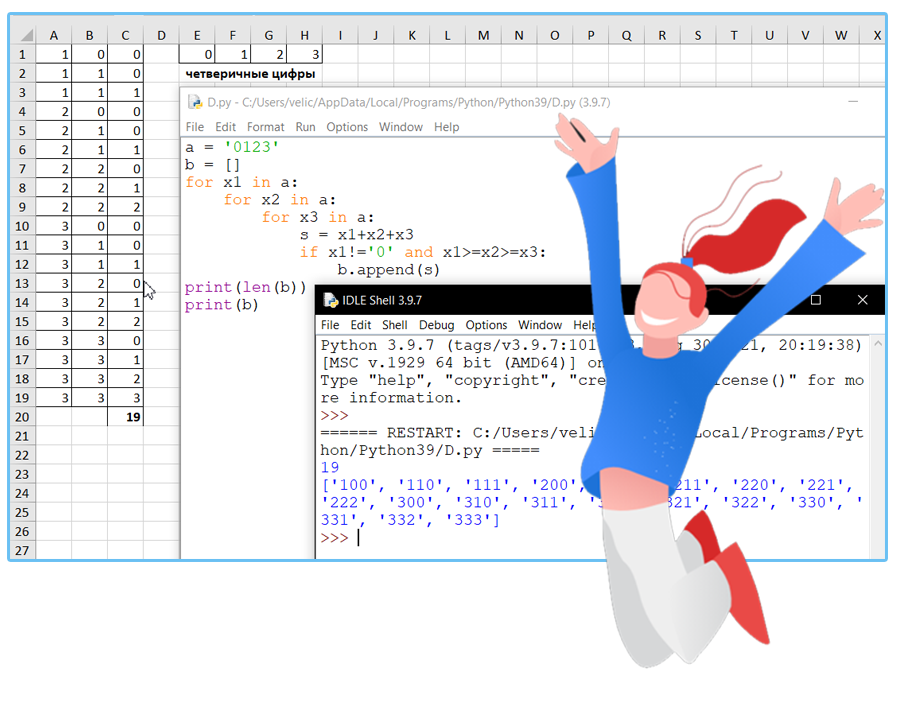
Ответ: 19
Вариант 12
Сколько существует различных трёхзначных чисел, записанных в пятеричной системе счисления, в записи которых цифры следуют слева направо в невозрастающем порядке?
Решение:
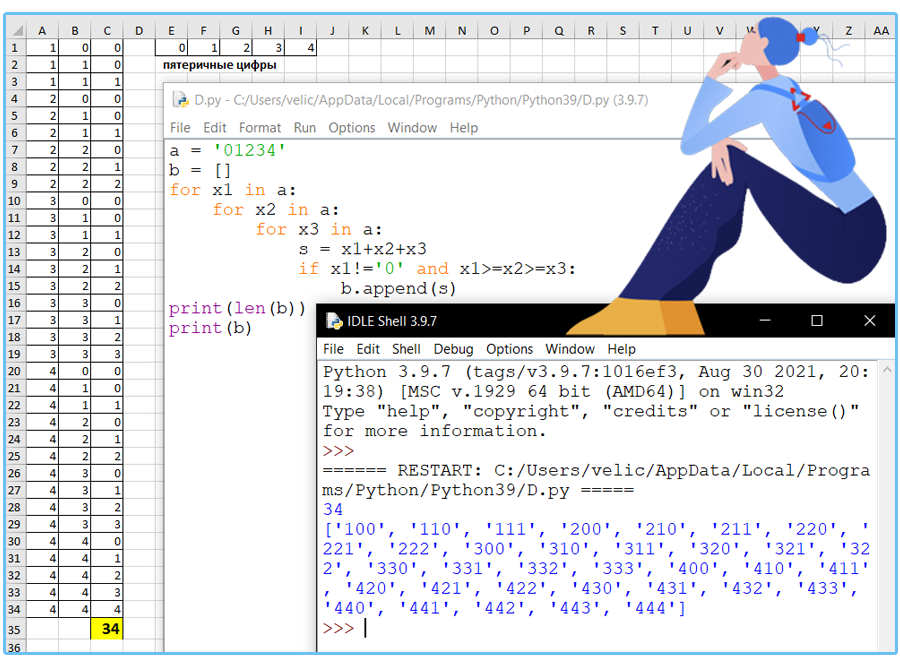
Ответ: 34
Вариант 13
Сколько существует различных четырёхзначных чисел, записанных в восьмеричной системе счисления, в записи которых есть ровно две одинаковых цифры, причём стоящие рядом?
Решение:
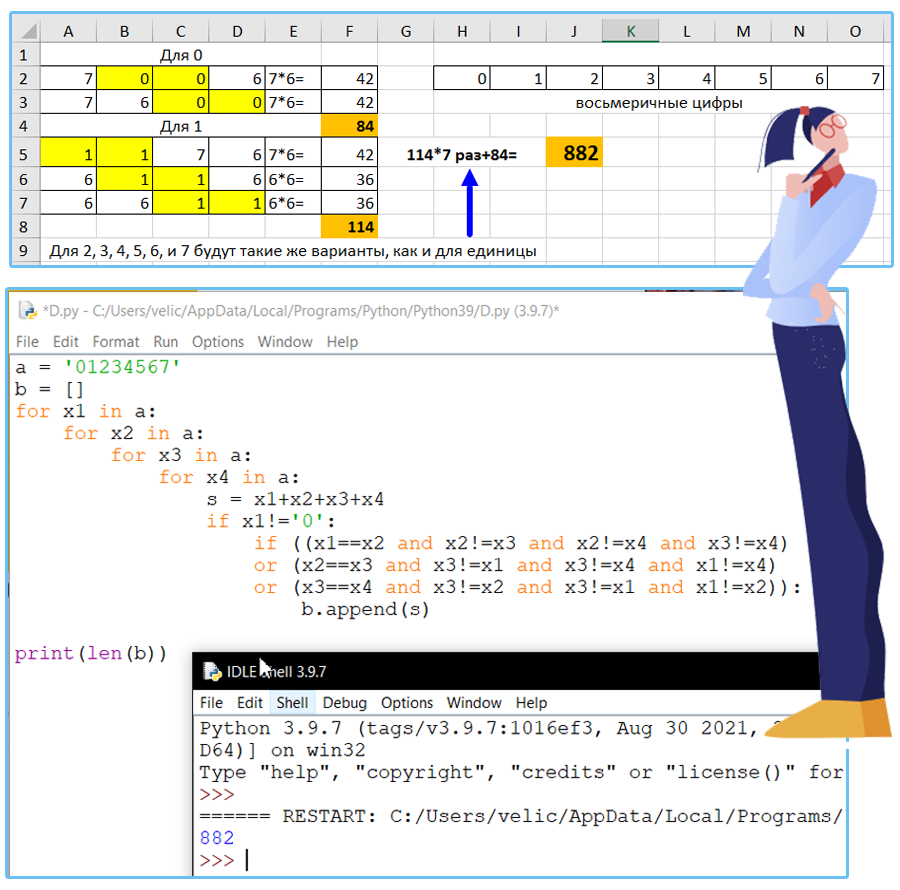
Ответ: 882
Вариант 14
Сколько существует различных четырёхзначных чисел, записанных в десятичной системе счисления, в записи которых есть ровно две одинаковых цифры, причём стоящие рядом?
Решение:
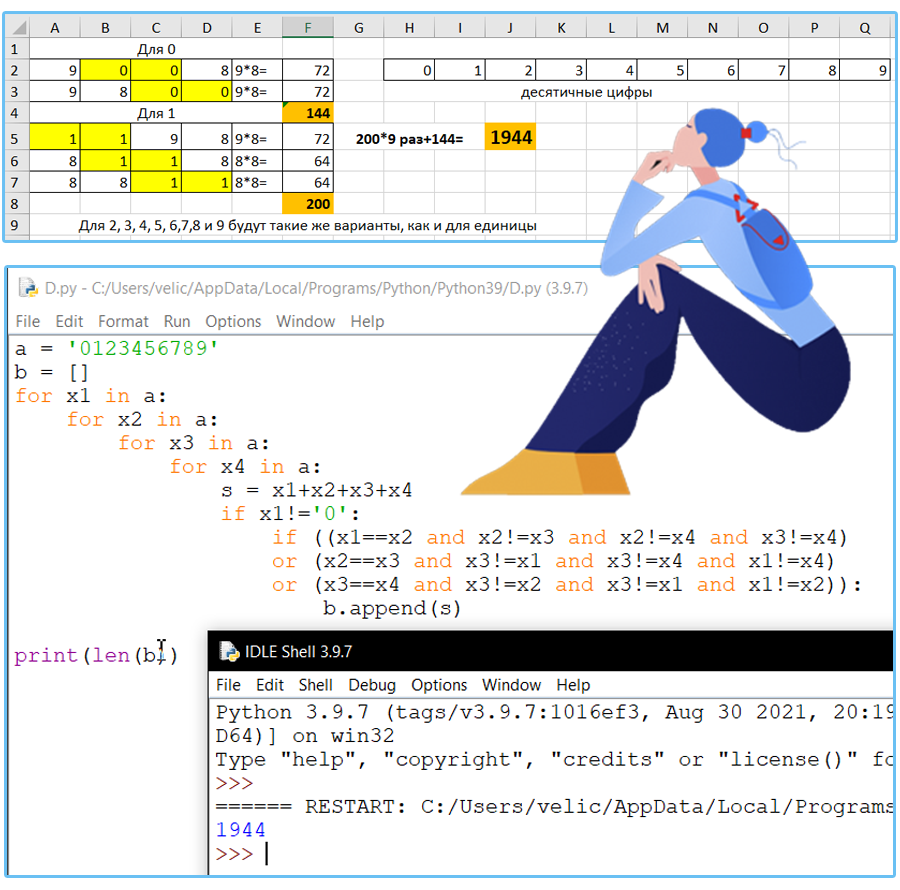
Ответ: 1944
Вариант 15
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которого является цифрой от 1 до 6. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно один раз, а каждая из других цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Решение:
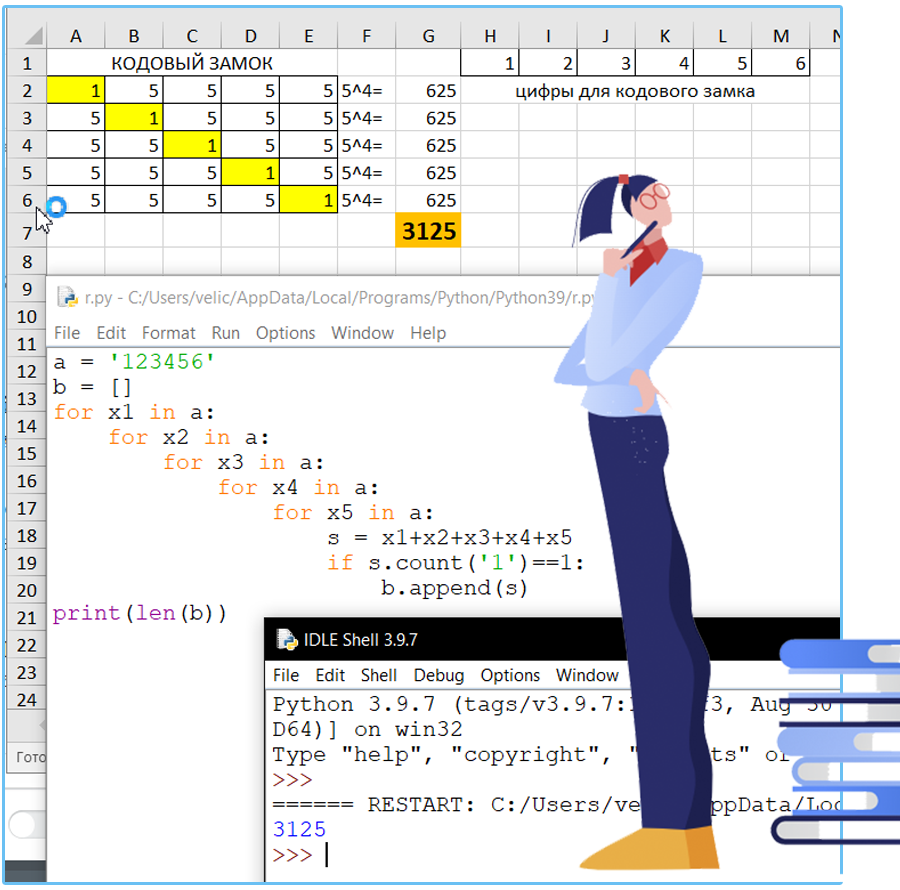
Ответ: 3125
Вариант 16
Шифр кодового замка представляет собой последовательность из трёх символов, каждый из которого является цифрой от 1 до 4. Сколько различных вариантов шифра можно задать, если известно, что цифра 2 должна встречаться в коде ровно один раз, а каждая из других цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Решение:
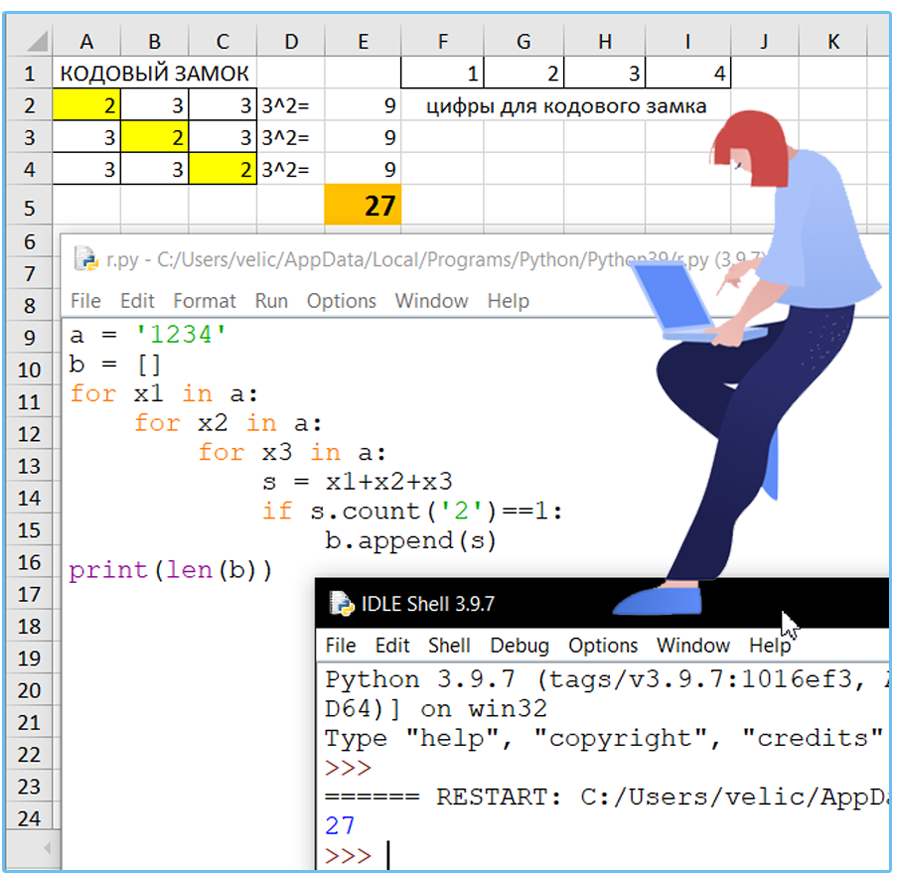
Ответ: 27
Вариант 17
Шифр кодового замка представляет собой последовательность из четырёх символов, каждый из которого является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 5 должна встречаться в коде ровно один раз, а каждая из других цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Ответ: 256
Вариант 18
Шифр кодового замка представляет собой последовательность из шести символов, каждый из которого является одной из букв А, В или С. Сколько различных вариантов шифра можно задать, если известно, что буква А должна встречаться в коде ровно один раз, а каждая из других букв может встречаться в шифре любое количество раз или не встречаться совсем?
Ответ: 192
Вариант 19
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которого является одной из букв X, Y или Z. Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно два раза, а каждая из других букв может встречаться в шифре любое количество раз или не встречаться совсем?
Ответ: 80
Вариант 20
Шифр кодового замка представляет собой последовательность из четырех символов, каждый из которого является одной из букв A, B, C или D. Сколько различных вариантов шифра можно задать, если известно, что буква A должна встречаться в коде ровно два раза, а каждая из других букв может встречаться в шифре любое количество раз или не встречаться совсем?
