
В задание №25
Тема: Обработка целых чисел. Проверка делимости
Проверяется умение создавать собственные программы (10–20 строк) для обработки целочисленной информации.
Немного теории:
Что нужно знать:
- в данных задачах нет ограничения на время выполнения, но отметим, что простой перебор иногда может выполняться в Phyton достаточно долго, поэтому необходимо написать эффективный алгоритм.
- задачи этого типа можно решать с помощью электронных таблиц или собственной программы;
k = 0
for n in range(a, b+1):
if условие выполнено:
k += 1
print( count ) if i % j == 0:
print("Делится")
else: print("Не делится") - проверку условия удобно оформить в виде функции, возвращающей логическое значение (True/False), но можно этого и не делать
- проверить делимость числа i на число j можно с помощью операции взятия остатка от деления i на j — если остаток == 0, число i делится на j нацело.
- ⇐ проверка делимости на языке Python выглядит так:
k = 0
for d in range(1, n+1):
if i % j == 0:
k += 1
print(k) # вывести количество делителей - для определения количества делителей натурального числа n можно использовать цикл, в котором перебираются все возможные делители d от 1 до n, при обнаружении делителя увеличивается счётчик делителей:
d = []
# перебор всех возможных делителей
for i in range(1,n+1):
if n % i == 0: # если нашли делитель d
d.append(i) # добавили его в массив - если требуется определить не только количество делителей, но и сами делители, нужно сохранять их в массиве
- в языке Python удобно использовать динамический массив: сначала он пуст, а при обнаружении очередного делителя этот делитель добавляется в массив:
- перебор делителей можно оптимизировать, учитывая, что наименьший из пары делителей, таких что a × b = n, не превышает квадратного корня из n; нужно только аккуратно обработать случай, когда число n представляет собой квадрат другого целого числа;
- отметим, что для чисел, которые предлагаются в вариантах заданий, такая оптимизация не обязательна; более того, усложнение программы может привести к дополнительным ошибкам…
nDel = 0 # количество делителей числа
for d in range(1, n+1): # все делители
if n % d == 0:
nDel += 1 # нашли ещё делитель
if nDel == 2:
print( "Число простое" )
else:
print( "Число составное" )
- простое число n делится только на 1 и само на себя, причём единица не считается простым числом; таким образом, любое простое число имеет только два делителя
- для определения простоты числа можно считать общее количество его делителей; если их ровно два, то число простое, если не два – не простое:
nDel = 0 # количество делителей числа
for i in range(1, n+1): # все делители
if n % i == 0:
nDel += 1 # нашли ещё делитель
if nDel > 2: # уже не простое число
break # досрочный выход из цикла
if nDel == 2:
print( "Число простое" )
else:
print( "Число составное" ) - работу программы можно ускорить: если уже найдено больше двух делителей, то число не простое и можно досрочно закончит работу цикла с помощью оператора break:
nDel = 0
for i in range(2, n):
if n % i == 0:
nDel += 1 # нашли делитель
break # досрочный выход из цикла
if nDel == 0:
print( "Число простое" )
else:
print( "Число составное" ) - другой вариант – считать количество делителей числа на отрезке [2; n–1]; как только хотя бы один такой делитель будет найден, можно завершить цикл, потому что число явно не простое:
prime = True # сначала считаем число простым
for d in range(2, n):
if n % d == 0:
prime = False # уже не простое
break # досрочный выход из цикла
if prime:
print( "Число простое" )
else:
print( "Число составное" )
- можно сделать то же самое с помощью логической переменной:
- в этом задании обычно предлагаются большие числа, поэтому проверка делимости на все числа от 2 до n-1 выполняется очень долго, и на устаревших компьютерах время работы приведённого выше алгоритма может быть слишком велико
- программу можно оптимизировать, если вспомнить, что наименьший из пары делителей, таких что a × b = n, не превышает квадратного корня из n; поэтому можно закончить перебор значением , округлив его до ближайшего целого числа ; если на отрезке [2;] не найден ни один делитель, их нет и на отрезке [+ 1, n – 1]
- следовательно, можно существенно ускорить перебор, изменив конечное значение переменной цикла:
С подключением библиотеки from math import sqrt
for d in range(2, round(sqrt(n))+1):
или без библиотеки
for d in range(2, round(n**0.5)+1):
Особенности языка Python
- (В. Ялдыгин) при записи больших чисел в Python можно использовать знаки подчеркивания; например, 7_777_777 обозначает то же самое, что и 7777777.
Пример задания:
Задание 1. Пять различных нечётных делителей
Тренировочный вариант №4 от 17 марта 2021 года СтатГрад Вариант ИН2010401
Решение:

- простой перебор будет в Phyton выполняться долго!!! поэтому обратимся к математике.
- любое число единственным образом (с точностью до порядка сомножителей) представимо в виде произведения простых чисел:
n = 2^k0 * p1^k1 * p2^k2 * ... * pi*ki,
где k0 — целое неотрицательное, k1, ..., ki — натуральные, p1, ..., pi — различные нечётные простые.
Любой делитель n конструируется как произведение простых из разложения выше. Сколько нечётных делителей мы можем сконструировать? (k1 + 1)(k2 + 1) ... (ki + 1). Это прозведение может быть равно пяти только если у числа ровно один нечётный простой делитель, который возводится в четвёртую степень.
Искомое число должно иметь вид:
n = 2k * p4
, гдеk — целое неотрицательное, p — нечетное простое. Сами нечётные делители тогда имеют вид 1, p, pp, ppp, pppp.
Источник: ИНФОРМАТИКА ЭКСПЕРТ >> 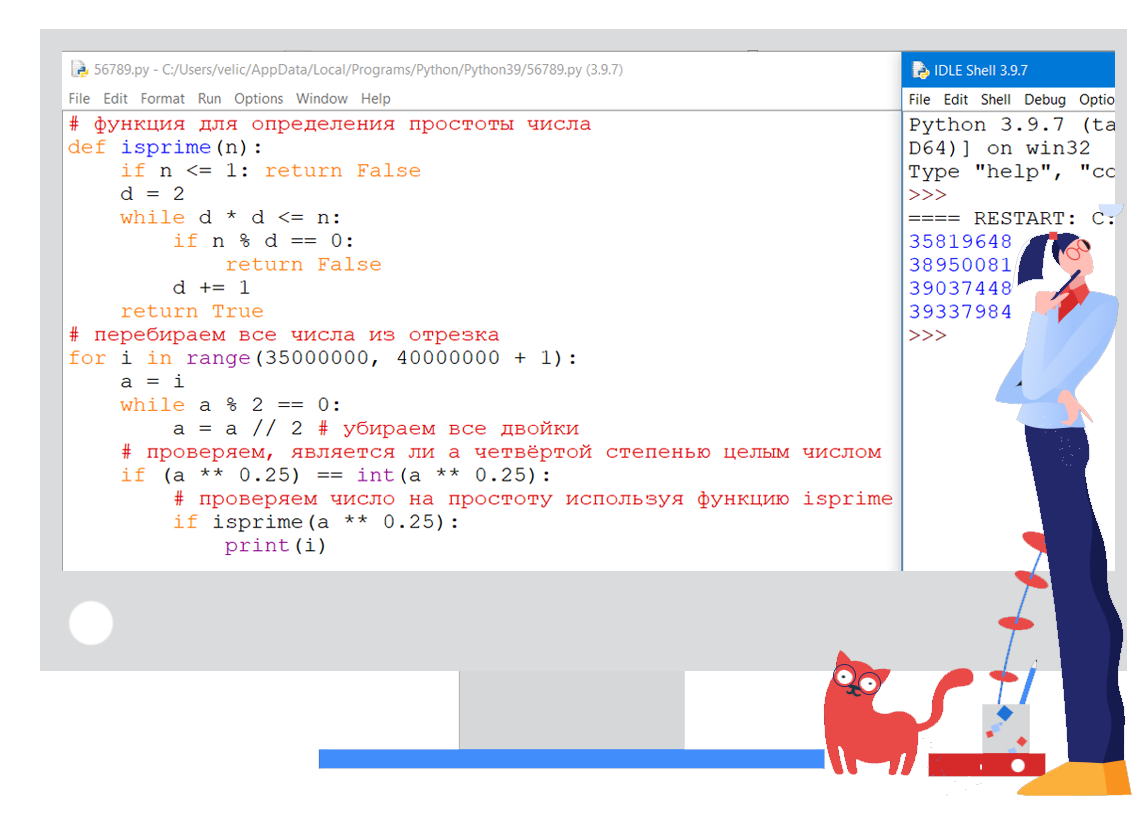
def isprime(n):
if n <= 1: return False
d = 2
while d * d <= n:
if n % d == 0:
return False
d += 1
return True
for i in range(35000000, 40000000 + 1):
a = i
while a % 2 == 0:
a = a // 2
if (a ** 0.25) == int(a ** 0.25):
if isprime(a ** 0.25):
print(i) ☆ Для тех, кто не любит набирать код 🙂

start, end = 35000000, 40000000
primes = [2]
for i in range(3, int(end**0.25) + 1, 2):
for d in range(2, int(i**0.5) + 1):
if i % d == 0:
break
else:
primes.append(i)
ans = []
for el in primes[1:]:
num = el**4
while num <= end:
if num >= start:
ans.append([num])
num *= 2
print(*sorted(ans), sep='\n') 1) Основная идея решения та же, но теперь будем перебирать не числа из отрезка, а простые числа. Если при возведении нечётного простого числа в четвёртую степень и умножении его на какую-либо степень двойки (в т.ч. нулевую), получится число, входящее в отрезок из условия, то оно пойдёт в ответ.
Ответ:
35819648
38950081
39037448
39337984
Задание 2. Ровно два делителя
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [174457; 174505], числа, имеющие ровно два различных натуральных делителя, не считая единицы и самого числа. Для каждого найденного числа запишите эти два делителя в два соседних столбца на экране с новой строки в порядке возрастания произведения этих двух делителей. Делители в строке также должны следовать в порядке возрастания.
Например, в диапазоне [5; 9] ровно два различных натуральных делителя имеют числа 6 и 8, поэтому для этого диапазона вывод на экране должна содержать следующие значения:
2 3
2 4
Решение (программа):
for i in range (174457, 174505+1):
k = 0
for j in range (2, i):
if i % j == 0:
k +=1
if k == 1: d1 = j
if k == 2: d2 = j
if k == 2:
print( d1, d2 )
ОЧЕНЬ БЫСТРО!!!
учитывая, что в этой задаче нас интересуют только два делителя, можно вместо массива использовать две дополнительных переменные, d1, если количество == 1, d2, если k == 2 🙂
ОТВЕТ:
3 58153
7 24923
59 2957
13 13421
149 1171
5 34897
211 827
2 87251
Решение (Ecxel):
Перебор можно организовать и с помощью электронных таблиц, используя функцию ОСТАТ (MOD) ;
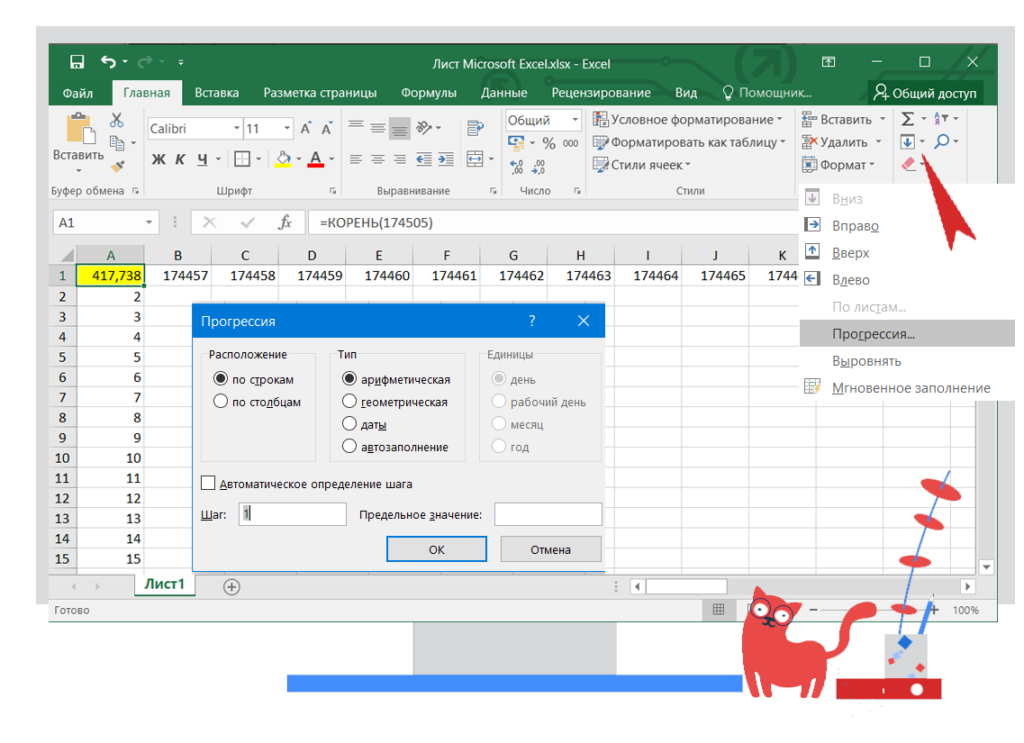
- найдем квадратный корень самого большого числа нашего отрезка, функция =КОРЕНЬ(174505)
- в первый столбец занесём все делители от 2 до квадратного корня из наибольшего числа 417
- в первую строку – все натуральные числа заданного отрезка
★ в Excel для этого можно использовать команду Заполнить — Прогрессия
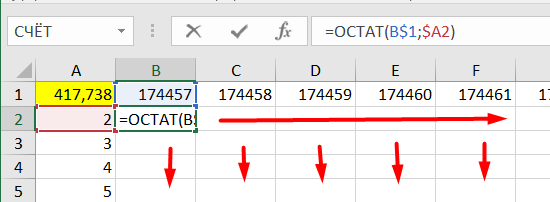
Начиная с B2, заполняем остатками от деления чисел из первой строки на делители из первого столбца;
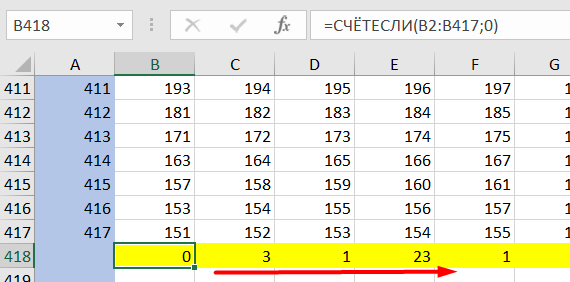
Ниже 417-й строки считаем для каждого числа количество делителей; нас интересуют числа, у которых один делитель на отрезке [2; 417]; используем функцию СЧЁТЕСЛИ, с помощью которой считаем нули в каждом столбце (ноль говорит о том, что число из первой строки разделилось нацело на делитель в первом столбце)
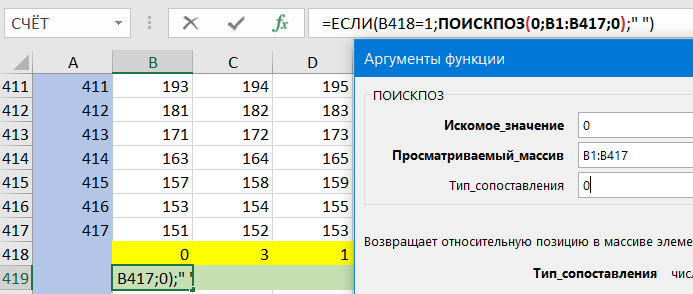
Для тех чисел, у которых всего один делитель, меньший или равный 417, находим его с помощью функции ПОИСКПОЗ; она находит в столбце 0 и определяет его позицию (третий аргумент функции ПОИСКПОЗ означает точное совпадение)
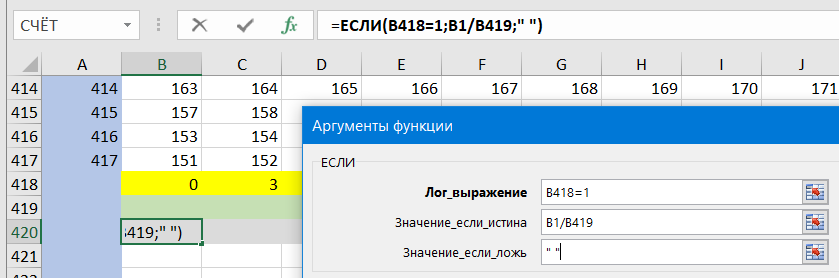
Теперь вычисляем второй делитель: делим число в первой строке на первый делитель, всё это только для подходящих чисел:
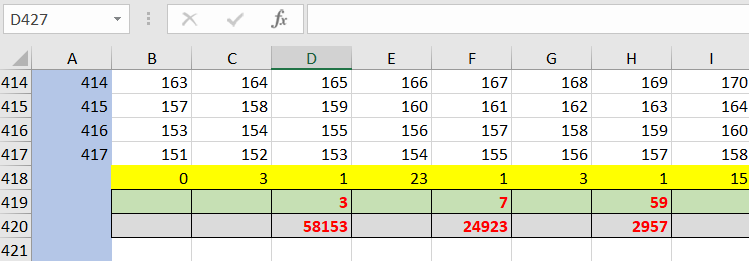
- Остаётся выписать найденные пары делителей
ОТВЕТ:
3 58153
7 24923
59 2957
13 13421
149 1171
5 34897
211 827
2 87251
Задание 3. Поиск простых чисел
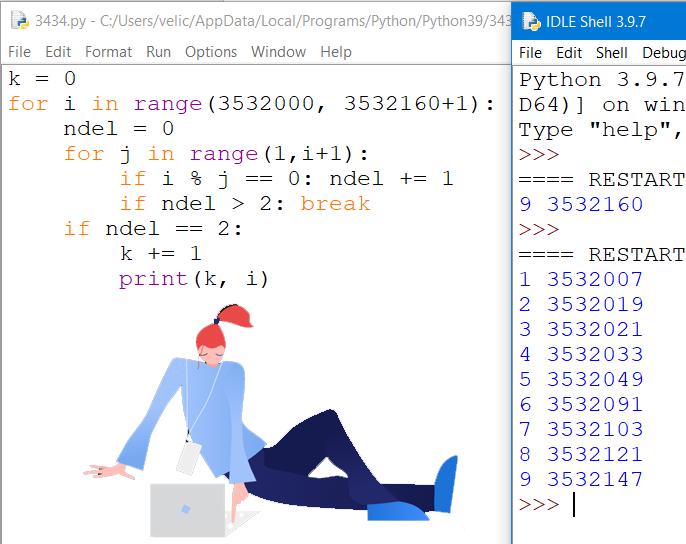
- поскольку нужно вывести не только сами числа, но и их порядковые номера, нужно использовать счётчик:
- простой перебор, может работать очень долго
- для определения простоты числа ищем полное количество делителей, если оно равно 2, то число простое:
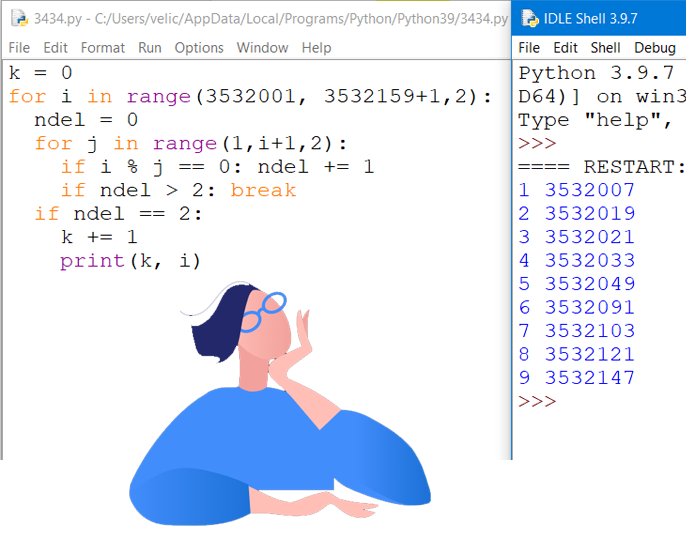
- идея ускорения времени выполнения программы состоит в том, что все простые числа, кроме 2 являются нечетными числами;
- тогда внешний цикл надо начинать не с числа 3532000, а с числа 3532001, при этом шаг цикла составит +2. Окончанием цикла также можно сделать не число 3532160, а 3532159;
- внутренний цикл также должен иметь шаг +2
k = 0
for i in range(3532000, 3532160+1):
ndel = 0
for j in range(1,i+1):
if i % j == 0: ndel += 1
if ndel > 2: break
if ndel == 2:
k += 1
print(k, i) k = 0
for i in range(3532001, 3532159+1,2):
ndel = 0
for j in range(1,i+1,2):
if i % j == 0: ndel += 1
if ndel > 2: break
if ndel == 2:
k += 1
print(k, i) Задание 4. Ровно четыре делителя
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [185 311; 185 330], числа, имеющие ровно четыре различных натуральных делителя. Для каждого найденного числа запишите эти четыре делителя в четыре соседних столбца на экране с новой строки. Делители в строке должны следовать в порядке возрастания.
Например, в диапазоне [12; 14] ровно четыре различных натуральных делителя имеет число 14, поэтому для этого диапазона вывод на экране должна содержать следующие значения:
1 2 7 14
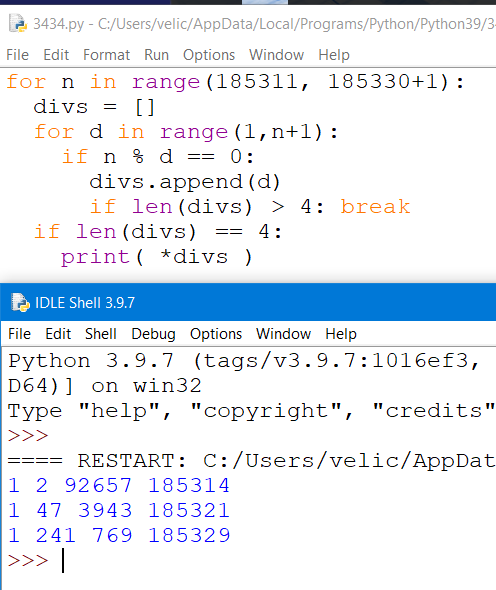
- заданный отрезок [194455; 194500] содержит не много чисел, будем решать перебором
- в качестве оптимизации можно прерывать работу внутреннего цикла, когда найден пятый делитель (число n уже точно не подходит), но это не критично
Задание 5. Шесть делителей и условие (большие числа)
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [50 000 000; 60 000 000], числа, имеющие ровно шесть различных натуральных делителей (не считая единицы и самого числа), среди которых есть число 911. В ответе запишите сначала количество таких чисел, а затем наименьшее из них.
Решение:
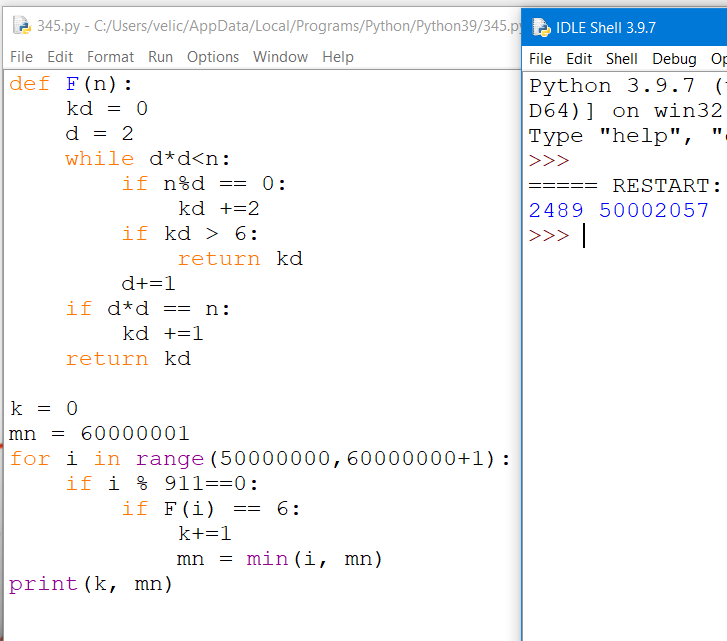
def F(n):
kd = 0
d = 2
while d*d 6:
return kd
d+=1
if d*d == n:
kd +=1
return kd
k = 0
mn = 60000001
for i in range(50000000,60000000+1):
if i % 911==0:
if F(i) == 6:
k+=1
mn = min(i, mn)
print(k, mn) Ответ: 2489 50002057

