Разбор варианта ЕГЭ информатика 2022
Кулабухов (Вариант 1)

Часть 2 (15-27)
Задание 15
На числовой оси даны два отрезка: X = [12; 93] и Y = [54; 150]. Укажите наименьшую возможную длину такого отрезка Z, для которого логическое выражение:
(x ∈ Y) → (¬(x ∈ X) ∧ ¬(x ∈ Z) → ¬(x ∈ Y))
Тождественно истинно (то есть принимает значение 1 при любом действительном значении переменной x).
Решение:

* Обратите внимание, 93 не входит в отрезок (93;150], но по условию нам необходимы любые действительные числа, поэтому 150-93=57!!! Как-то не очень правильно 🙁
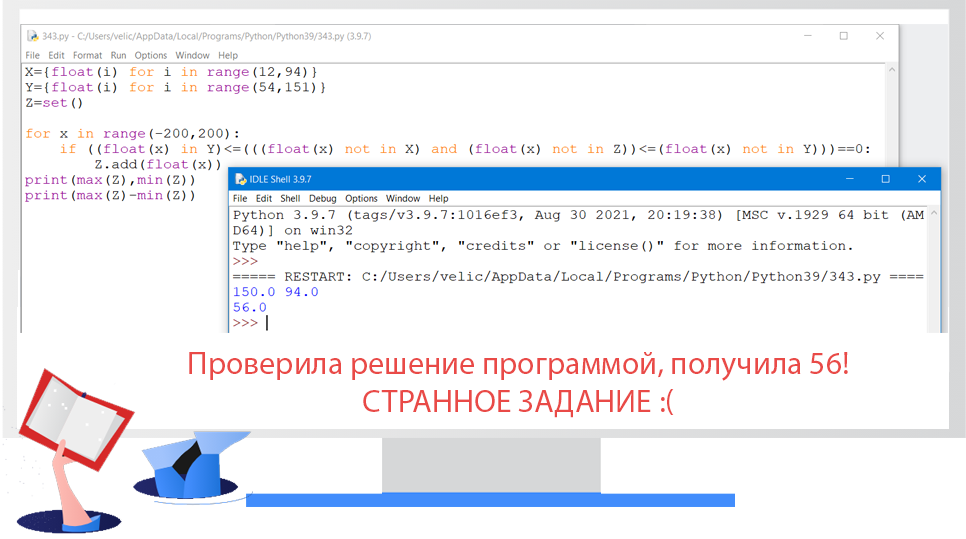
Ответ: в сборнике ответ - 57
Задание 16
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими отношениями:
F(1) = 1;
F(n) = n + F(n/2), если n чётно;
F(n) = n * F(n -1), если n>1 и при этом n нечётно.
Чему равно значение функции F(37)?
Решение:
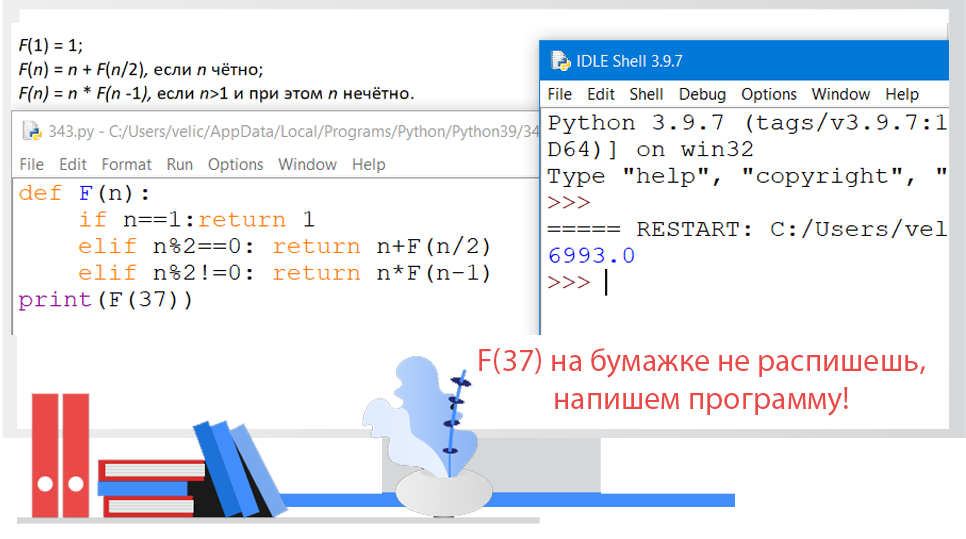
Ответ: 6993
Задание 17
Решение:
Для выполнения этого задания необходимо:
- Скачать файл, создать папку и перенести его в эту папку;
- Создать файл для программы и сохранить его тоже в эту папку;
- Прочитать внимательно задание.
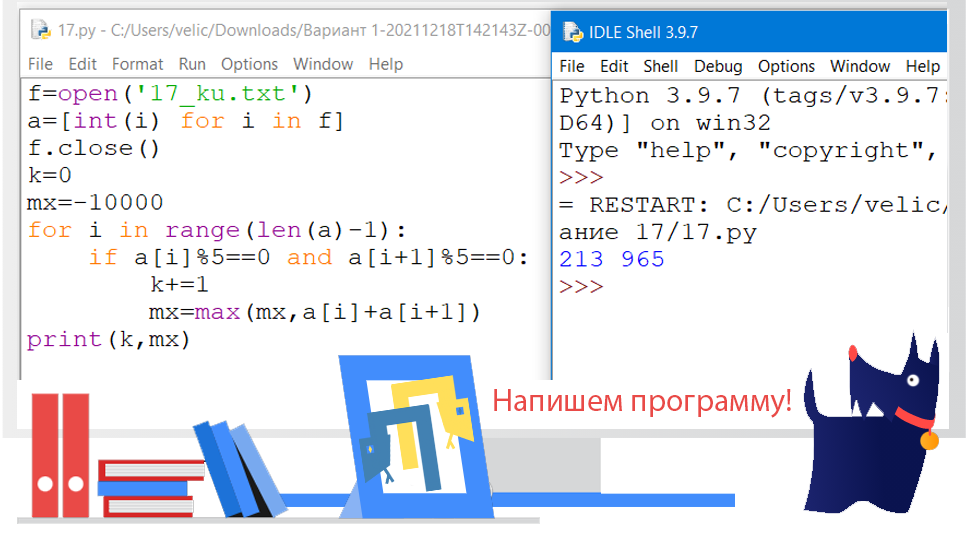
Ответ: 213 965
Задание 18
Решение:
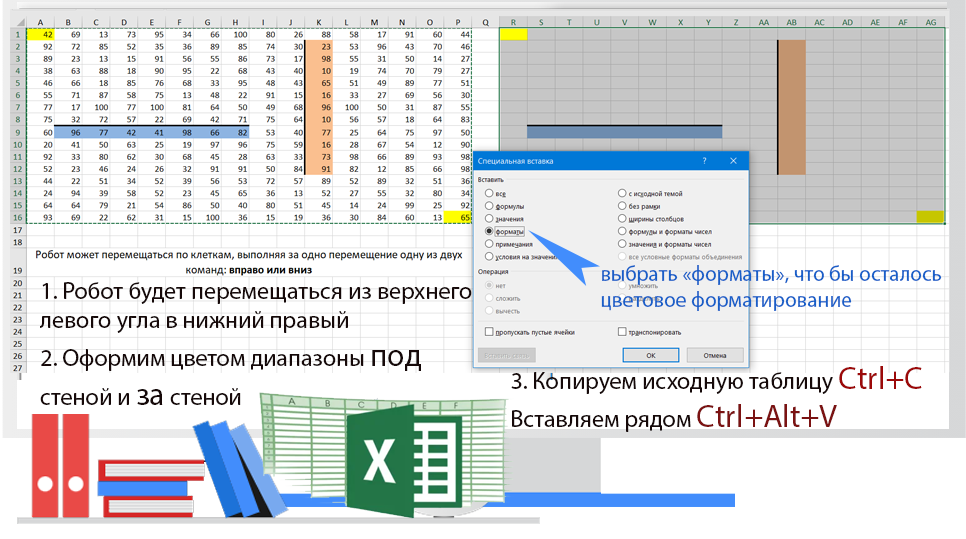
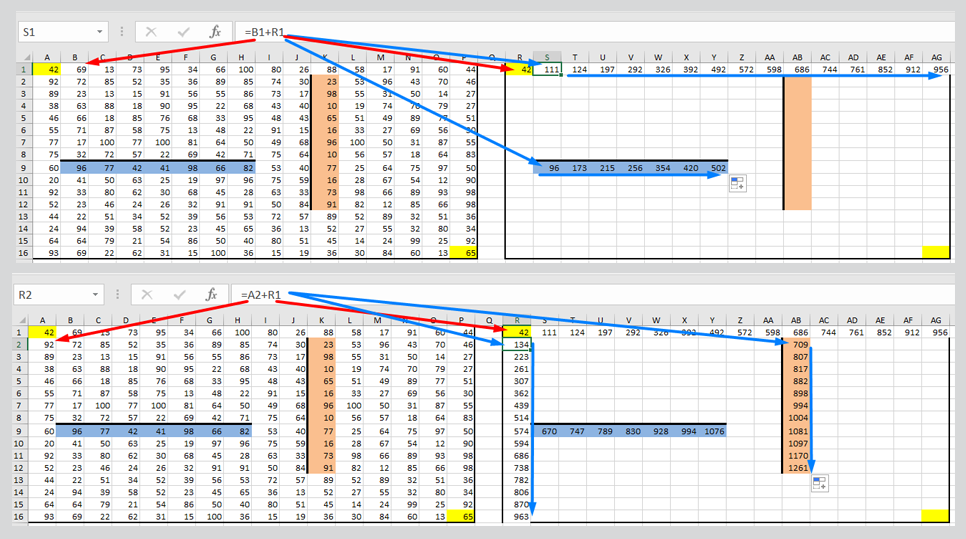
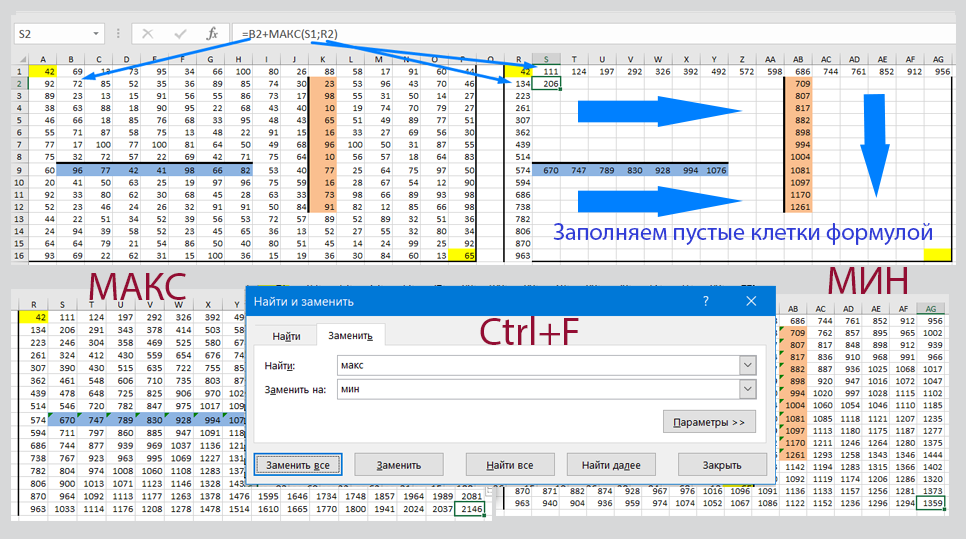
Ответ: 2146 1359
Задание 19
- Добавить в кучу один камень или
- Добавить в кучу три камня или
- Увеличить количество камней в куче в четыре раза.
Игра завершается в тот момент, когда количество камней в куче становится не менее 78. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 78 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 77.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:

Ответ: 5
Задание 20
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Теперь попробуем определить значение S, при которых у Пети будет выигрышная стратегия, причём Петя не сможет выиграть первым ходом, но сможет выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.

Ответ: 16 18
Задание 21
- У Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
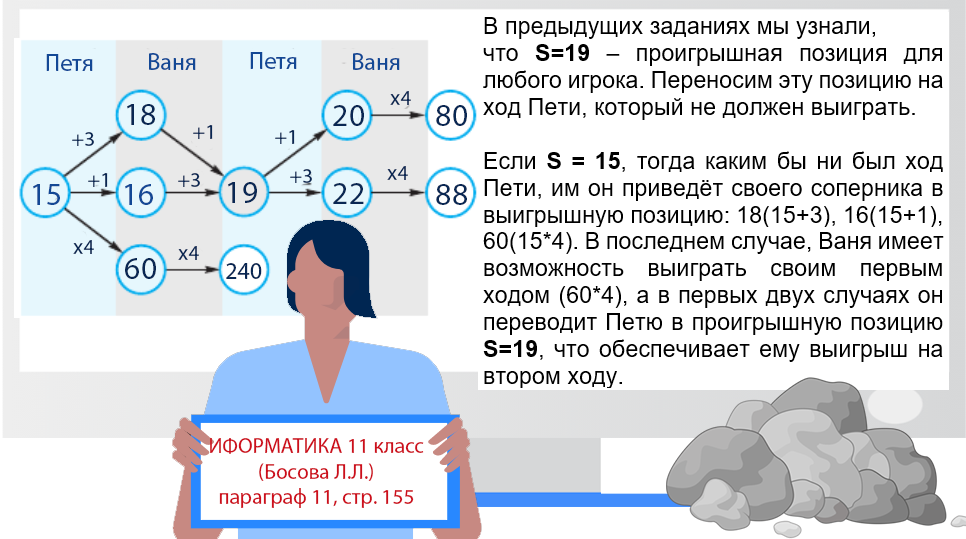
Ответ: 15
Задание 22
Ниже на четырех языках программирования записан алгоритм. Получив на вход число x, это алгоритм печатает число M. Известно, что x < 480. Укажите такое (то есть меньше 480) наибольшее число х, при вводе которого алгоритм печатает 12.
Решение:
X = int(input())
L=X
M=132
if L % 2 != 0:
M=64
while L != M:
if L >M:
L -= M
else:
M -= L
print(M)
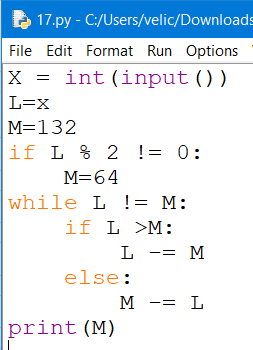
Составим программу на языке Phyton для перебора значений переменной x<480 и выполнения для каждого значения заданного алгоритма. Выведем наибольшее значение, при котором получится М=12.
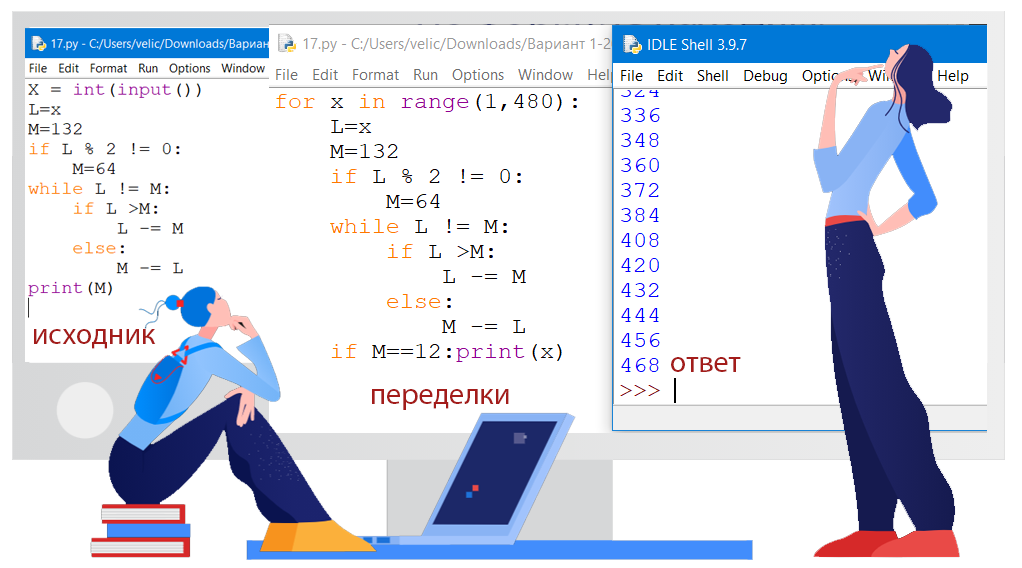
Ответ: 468
Задание 23
- Прибавить 1
- Умножить на 2
- Умножить на 5
Например, для программы 2231 при исходном числе 5 траектория будет состоять из чисел 10, 20, 100, 1001.
Решение:

Ответ: 36
Задание 24
Решение:
Для выполнения этого задания необходимо:
- Скачать файл, создать папку и перенести его в эту папку;
- Создать файл для программы и сохранить его тоже в эту папку;
- Прочитать внимательно задание.
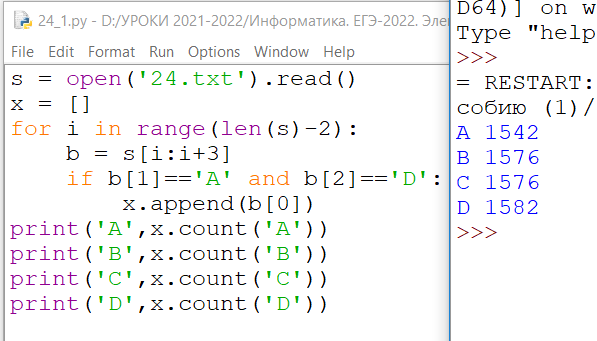

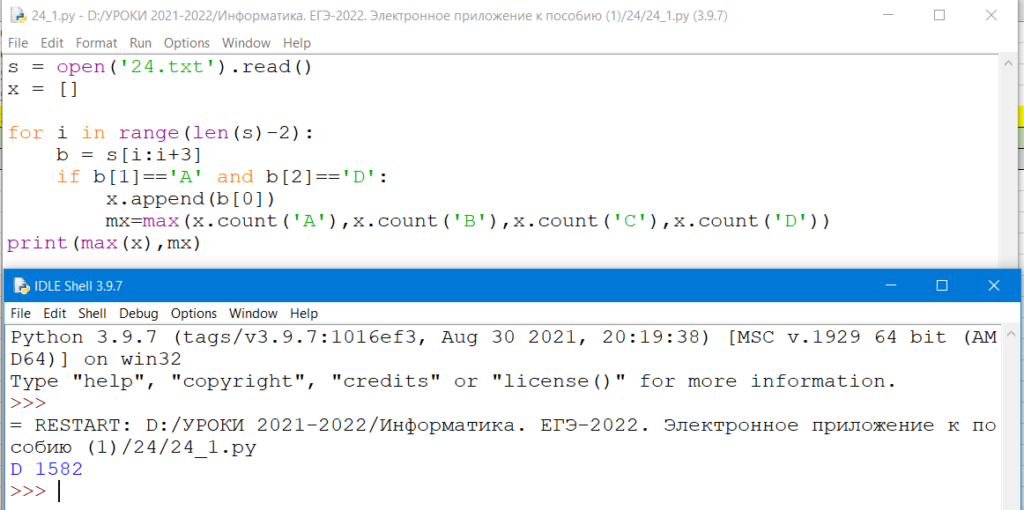
Ответ: D 1582
Задание 25
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [50 000 000; 60 000 000], числа, имеющие ровно шесть различных натуральных делителей (не считая единицы и самого числа), среди которых есть число 911. В ответе запишите сначала количество таких чисел, а затем наименьшее из них.
Решение:
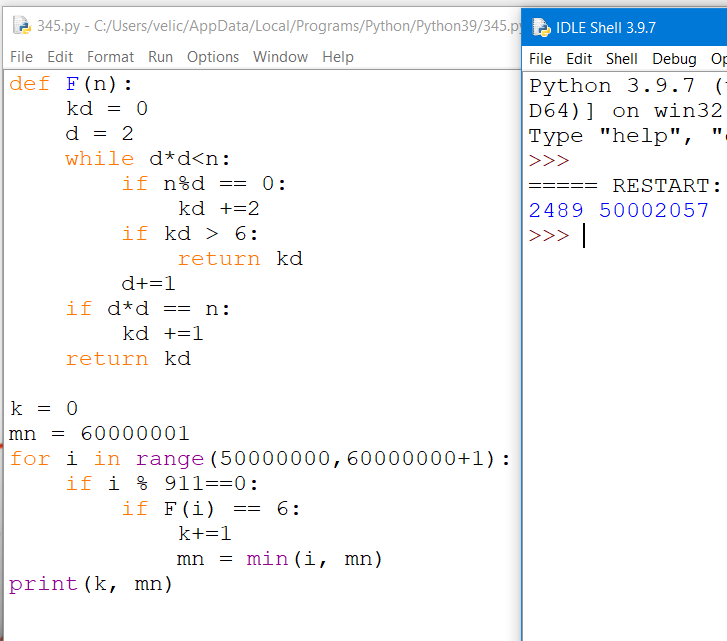
def F(n):
kd = 0
d = 2
while d*d 6:
return kd
d+=1
if d*d == n:
kd +=1
return kd
k = 0
mn = 60000001
for i in range(50000000,60000000+1):
if i % 911==0:
if F(i) == 6:
k+=1
mn = min(i, mn)
print(k, mn) 