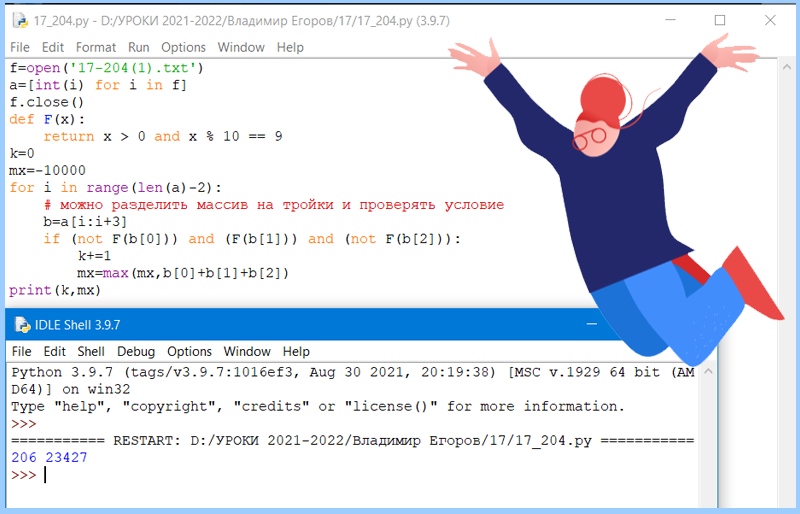
В задание №17 добавлен файл. Он содержит последовательность целых чисел, которую необходимо будет использовать для обработки массива. Также в задании есть пример решения для другой последовательности. В ответ потребуется записать пару чисел, требуемую по условиям задачи.
Задание 17 проверяет умение написать простую переборную программу, на языке программирования, содержащую циклы и ветвление. Это задание проверяет только технические программистские умения, так как сам алгоритм решения описан в постановке задачи.
В отличии от 2021 года, в 2022 году к заданию 17 будет прилагаться файл данных. Отдельной технической задачей является чтение этого файла. Ответ будет зависеть от исходных данных.
Решением будет являться алгоритм последовательного просмотра пар.
Вариант 1. В данных задачах под парой подразумевается два идущих подряд элемента последовательности.
ДЕМО-вариант
В файле 17-demo1.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от −10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число делится на 3, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности. Например, для последовательности из пяти элементов: 6; 2; 9; –3; 6 — ответ: 4 11.
Решение:
- Cкачать файл, создать папку и перенести его в эту папку;
- Создать файл для программы и сохранить его тоже в эту папку;
- Прочитать внимательно задание.
Описание программы:
Python может с относительной легкостью обрабатывать различные форматы файлов: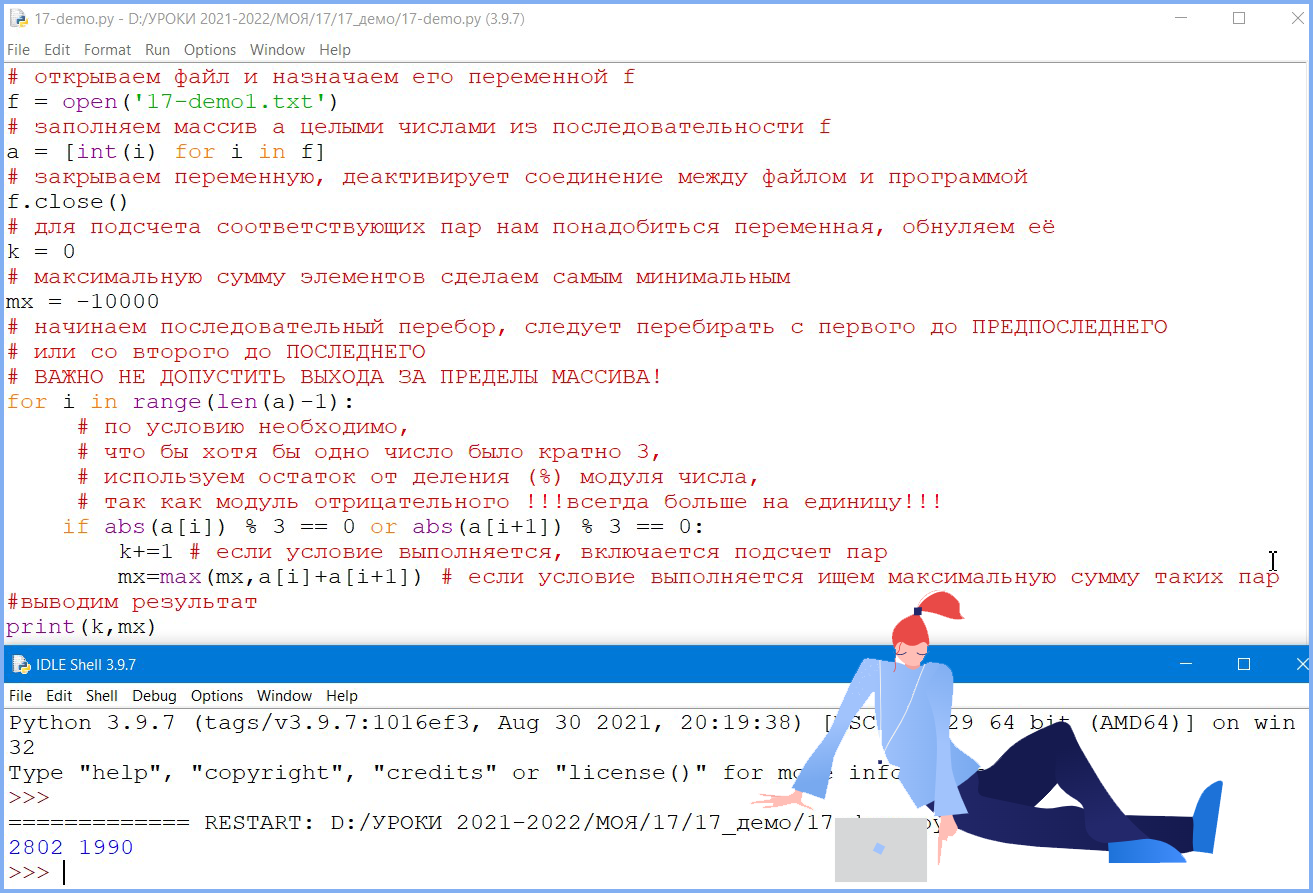
f = open('17-demo1.txt')
a = [int(i) for i in f]
f.close()
k = 0
mx = -10000
for i in range(len(a)-1):
if abs(a[i]) % 3 == 0 or abs(a[i+1]) % 3 == 0:
k+=1
mx=max(mx,a[i]+a[i+1])
print(k,mx)
Ответ: 2802 1990
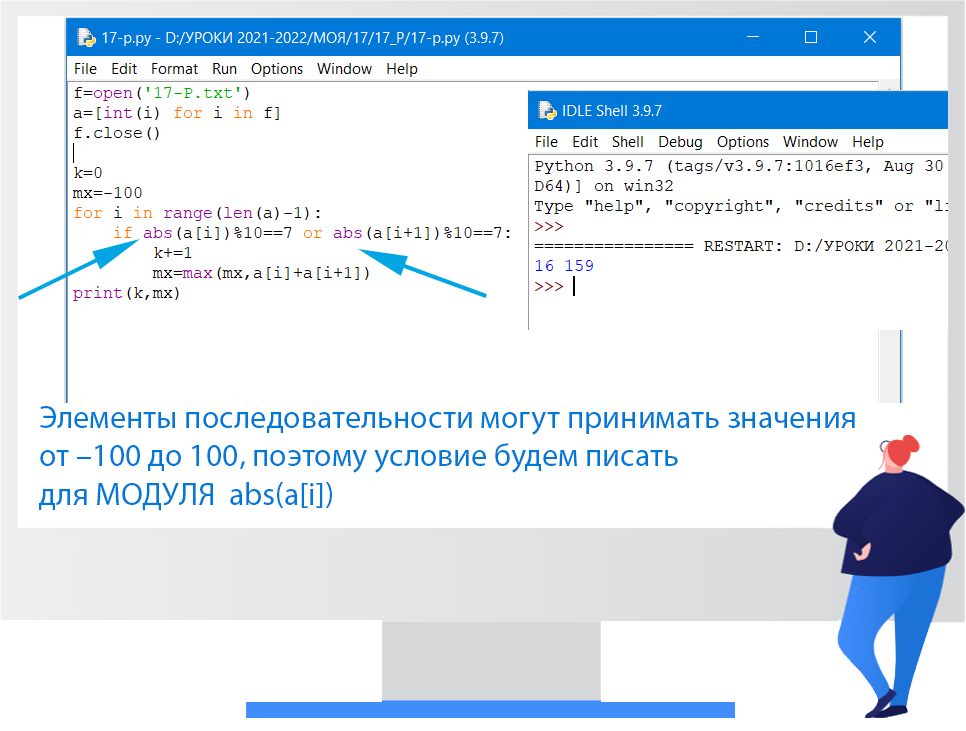
Ответ: 16 159
Проверим задачу в Excel
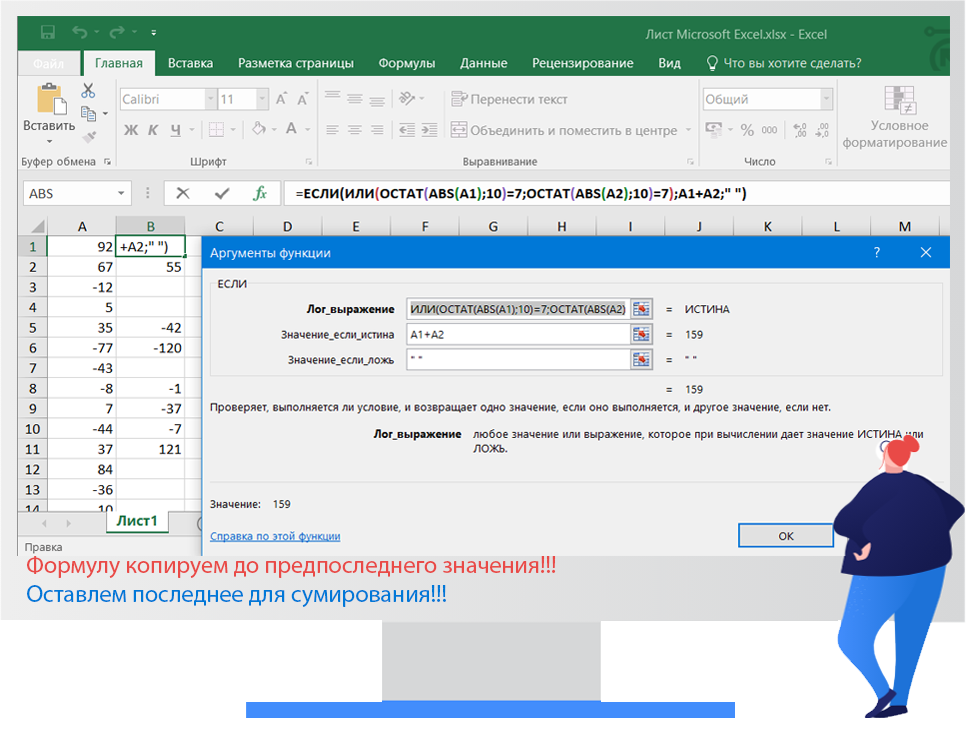
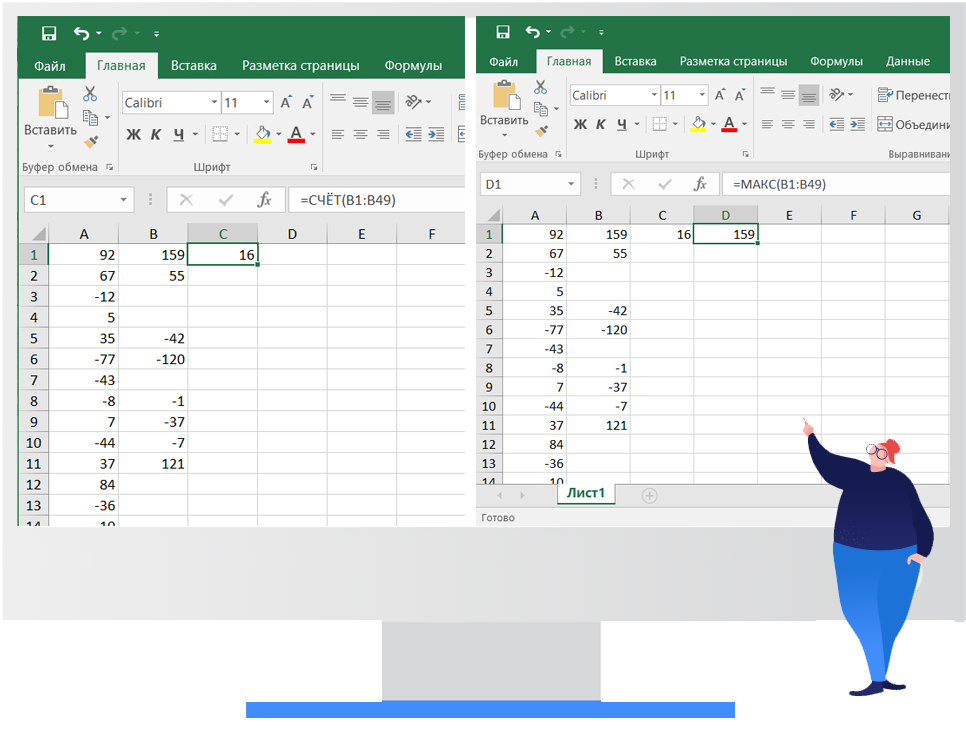
Ответ: 16 и 159
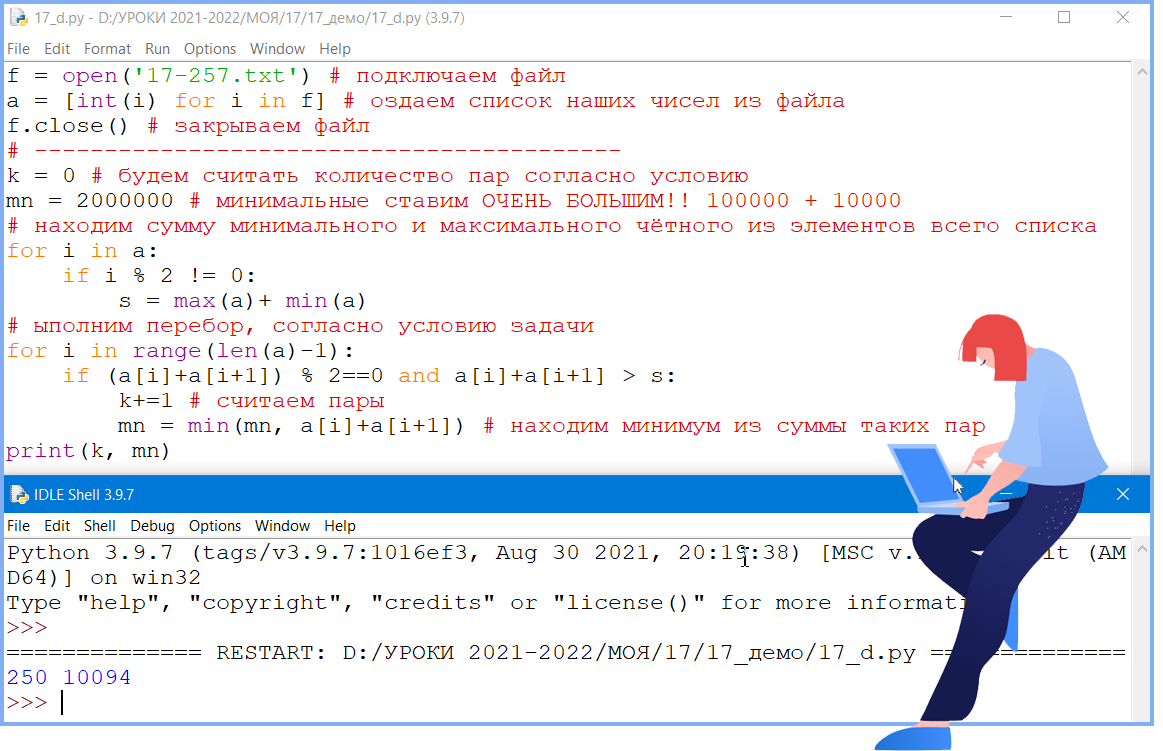
f = open('17-257.txt')
a = [int(i) for i in f]
f.close()
k = 0
mn = 2000000
for i in a:
if i % 2 != 0:
s = max(a)+ min(a)
for i in range(len(a)-1):
if (a[i]+a[i+1]) % 2==0 and a[i]+a[i+1] > s:
k+=1
mn = min(mn, a[i]+a[i+1])
print(k, mn)
Ответ: 250 10094
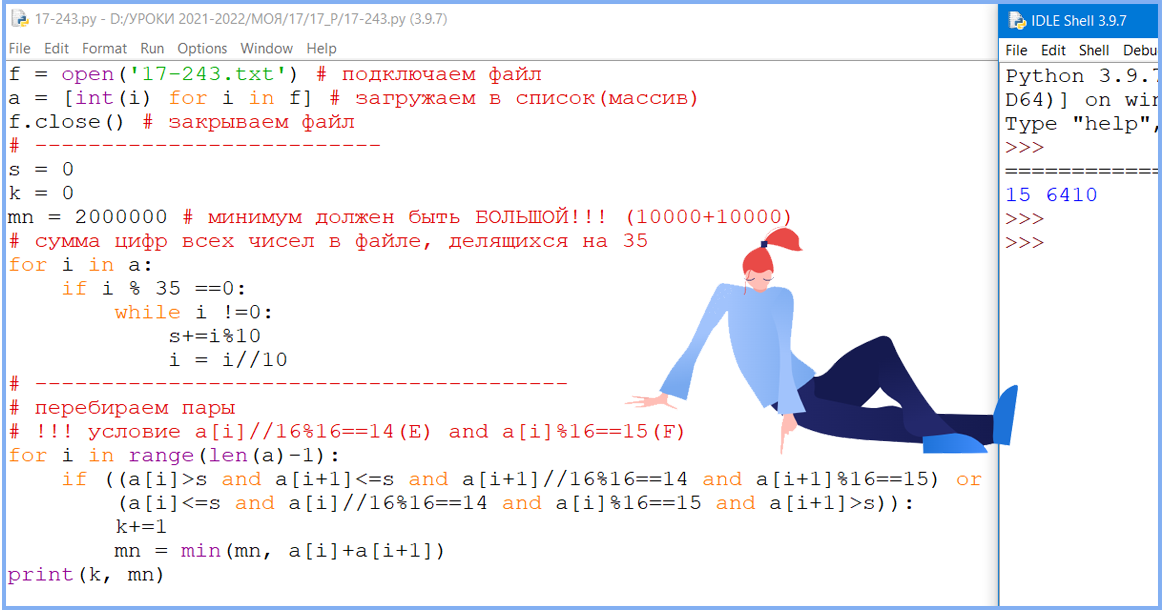
f = open('17-243.txt')
a = [int(i) for i in f]
f.close()
s = 0
k = 0
mn = 2000000
for i in a:
if i % 35 ==0:
while i !=0:
s+=i%10
i = i//10
for i in range(len(a)-1):
if (a[i]>s and a[i+1]<=s and a[i+1]//16%16==14 and a[i+1]%16==15) or (a[i]<=s and a[i]//16%16==14 and a[i]%16==15 and a[i+1]>s)):
k+=1
mn = min(mn, a[i]+a[i+1])
print(k, mn)
Ответ: 15 6410
Вариант 2. В данных задачах под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.
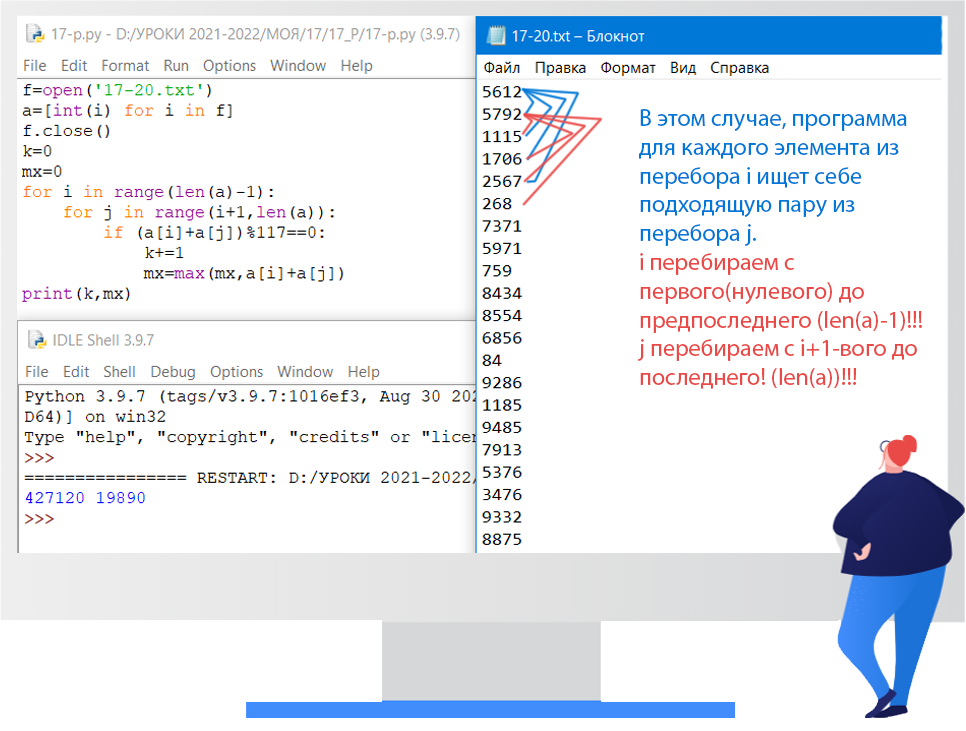
f = open('17-20.txt')
a = [int(i) for i in f]
f.close()
k = 0
mx = 0
for i in range(len(a)-1):
for j in range(i+1,len(a)):
if (a[i] + a[j]) % 117 == 0:
k+=1
mx=max(mx,a[i]+a[j])
print(k, mx)
Ответ: 427120 и 19890
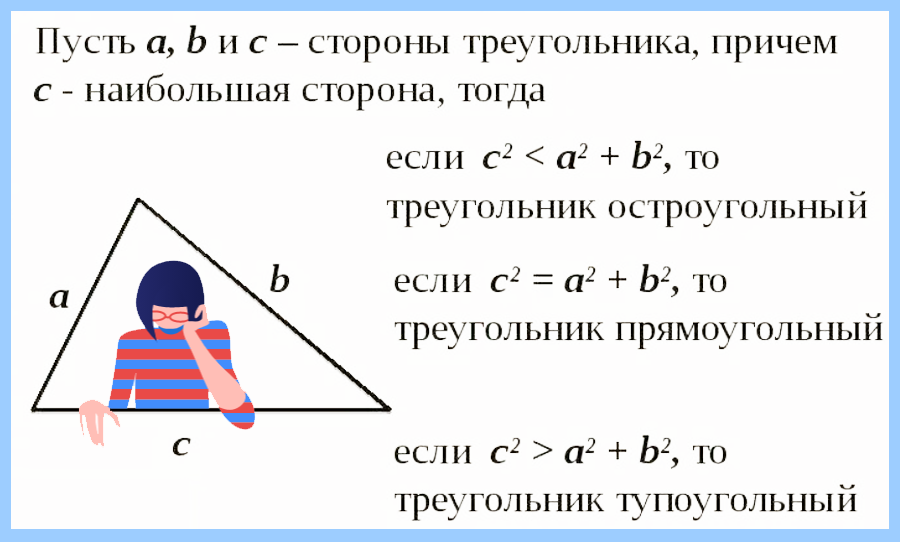
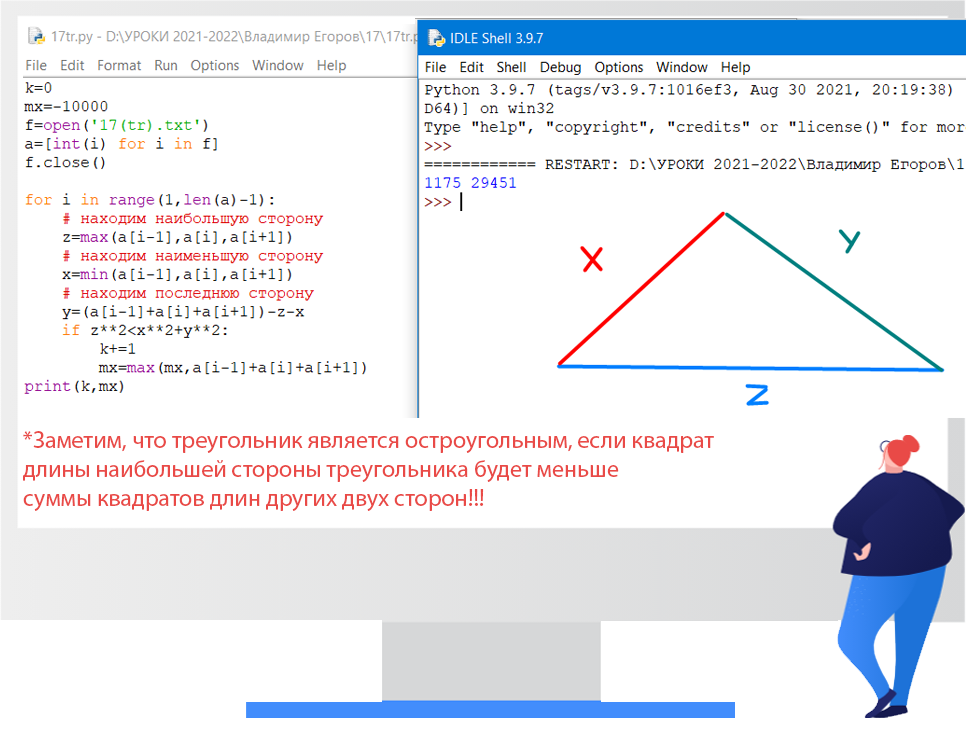
Вариант 3. В данных задачах считаем тройки элементов идущих подряд выполняя условие