Задание 16. Рекурсивный алгоритм

Училка
11.10.2022
"Поколение Python": курс для начинающих
Задание 16. Вычисление рекуррентных выражений

В программировании рекурсия, или же рекурсивная функция — это такая функция, которая вызывает саму себя.

Рекурсивные функции с возвращаемыми значениями
Задание 6 (ИНФ-11 ЕГЭ 2023_ДЕМО)

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?

Вариант программы 1
Лимит рекурсии по умолчанию в Python является 1000, вы получите ошибку « RecursionError: максимальная глубина рекурсии превышена в сравнении »
Это может быть исправлено, увеличивая предел рекурсиона в Python, ниже – фрагмент о том, как вы можете увеличить предел рекурсии.
import sys
sys.setrecursionlimit(2030)
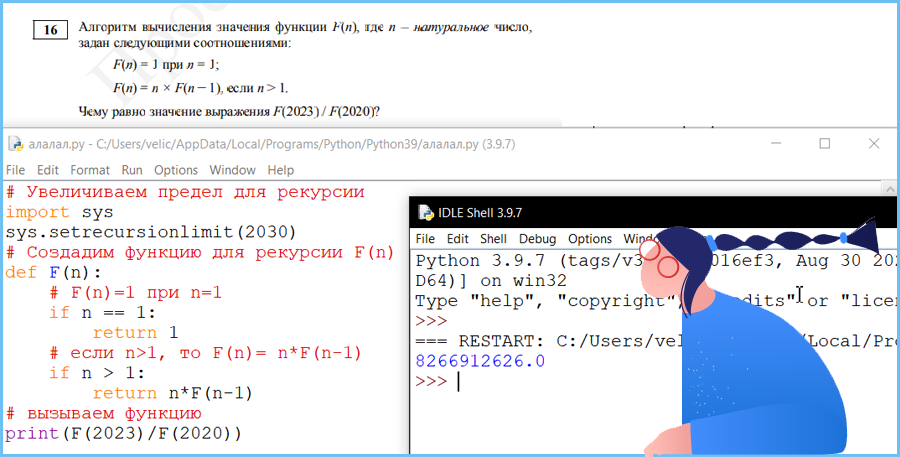
Вариант программы 2
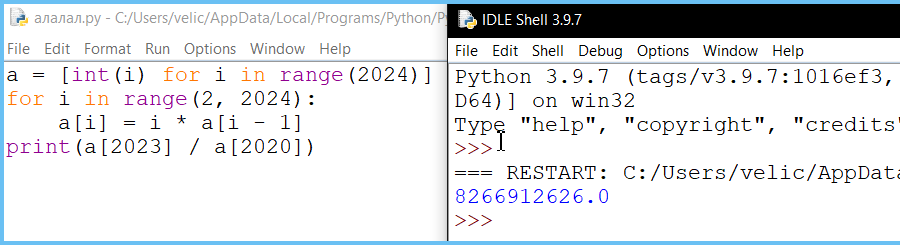
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Решу ЕГЭ)

Последовательность чисел Падована задается рекуррентным соотношением:

F(1) = 1

F(2) = 1

F(3) = 1

F(n) = F(n–3) + F(n–2), при n >3, где n – натуральное число.

Чему равно двенадцатое число в последовательности Падована?

В ответе запишите только натуральное число.

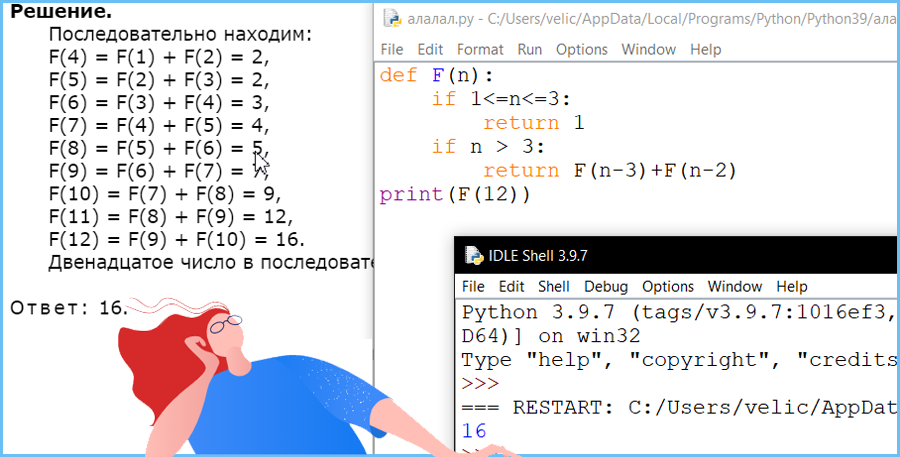
Задание 6 (Решу ЕГЭ)

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

 

F(1) = 1;

F(n) = n + F(n − 2), если n — нечётно, и n > 1;

F(n) = n × F(n − 1), если n — чётно.

 

Чему равно значение функции F(60)?

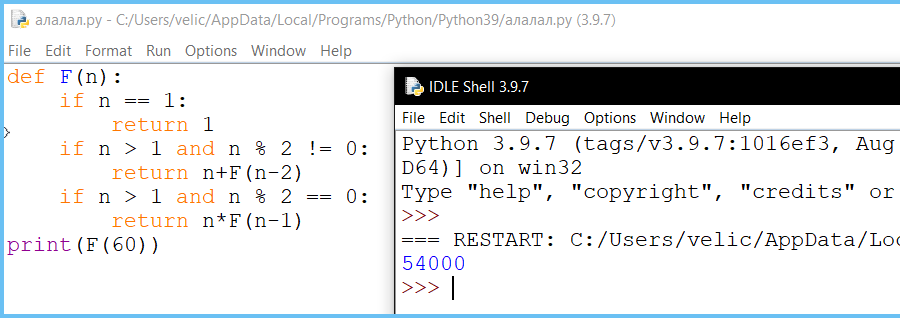
Алгоритмы, опирающиеся на несколько предыдущих значений
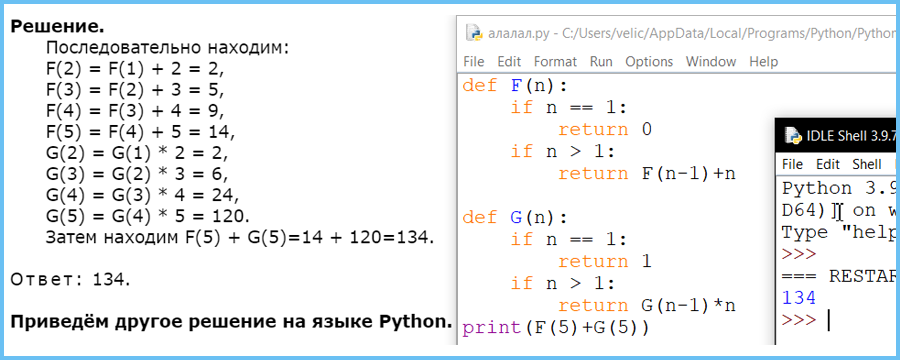
Задание 6 (Решу ЕГЭ)

Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 0

F(n) = F(n–1) + n, при n >1

G(1) = 1

G(n) = G(n–1) * n, при n >1

Чему равно значение функции F(5) + G(5)?

В ответе запишите только натуральное число.

Сложные задачи
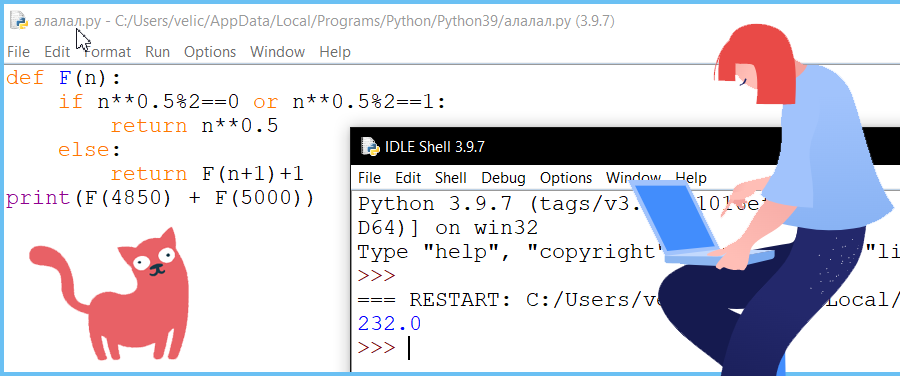
Задание 6 (Поляков ЕГЭ)
(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = sqrt(n), если sqrt(n) – натуральное число, F(n) = F(n + 1) + 1, если sqrt(n) – дробное число. Чему равно значение выражения F(4850) + F(5000)?
При делении натурального числа на 2 мы получаем в остатке (%) или 0 или 1 (чётные и нечётные числа), таким образом проверяем, если корень дает четное или нечётное целое число, то выводим корень этого числа во всех остальных случаях применяет функцию F(n+1)+1
sqrt(n) запишем как n**0.5, что бы не подключать дополнительный математический модуль из библиотеки
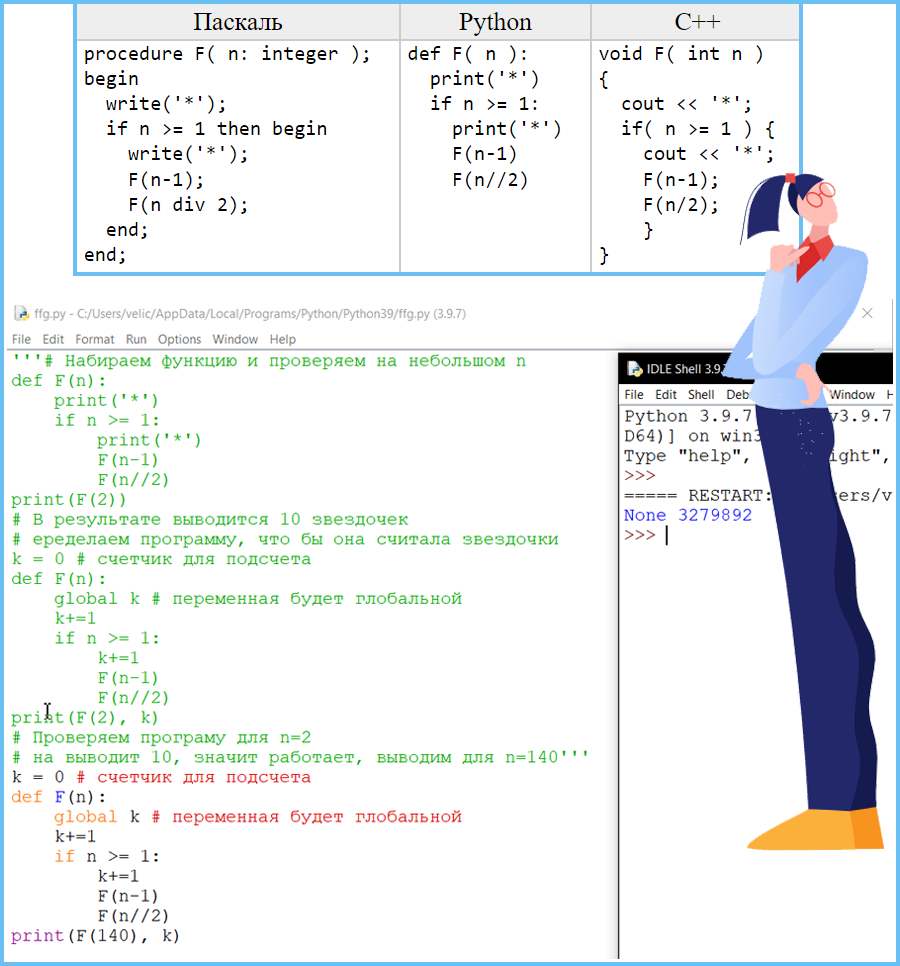
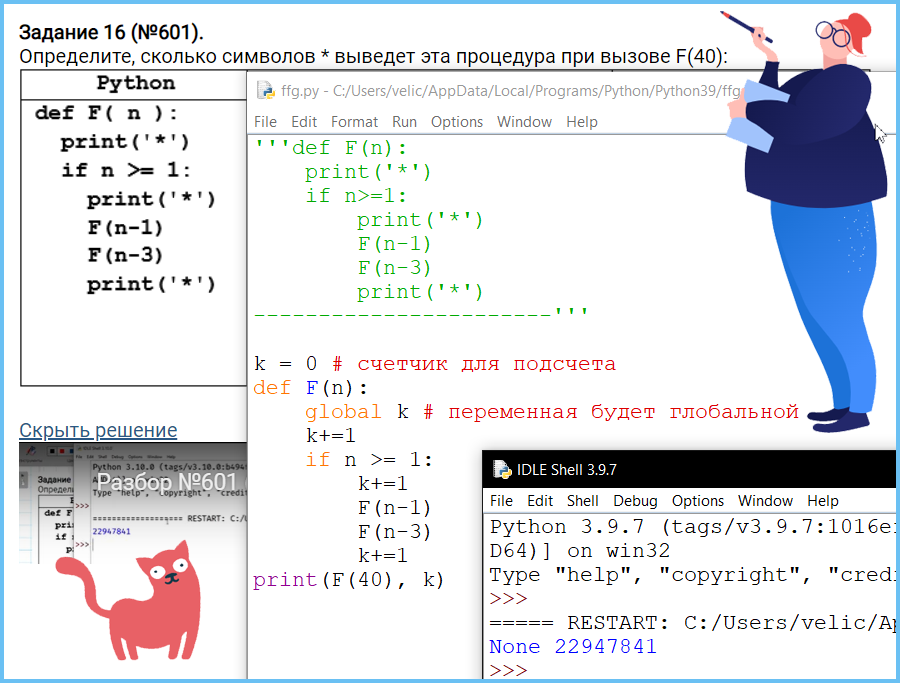
Задание 6 (Поляков ЕГЭ)

Определите, сколько символов * выведет эта процедура при вызове F(140):

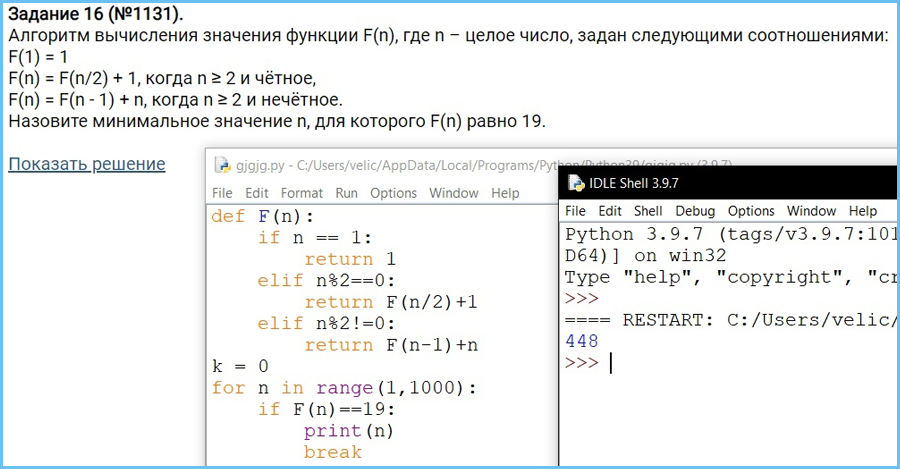
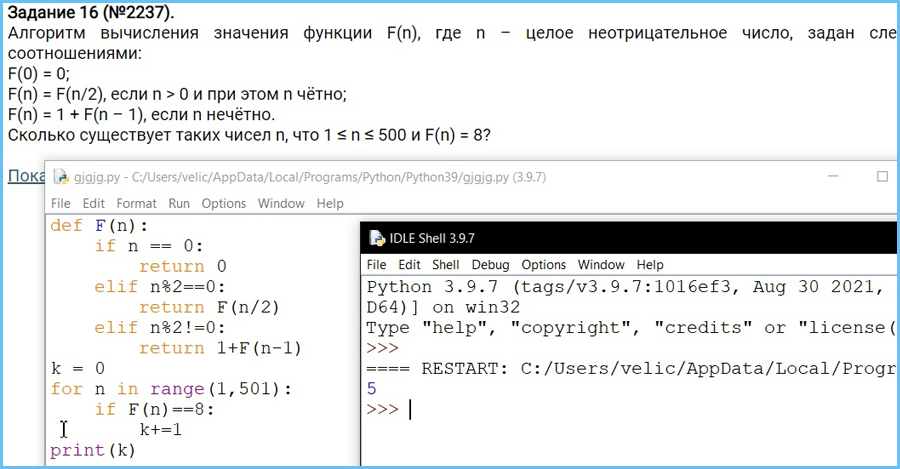
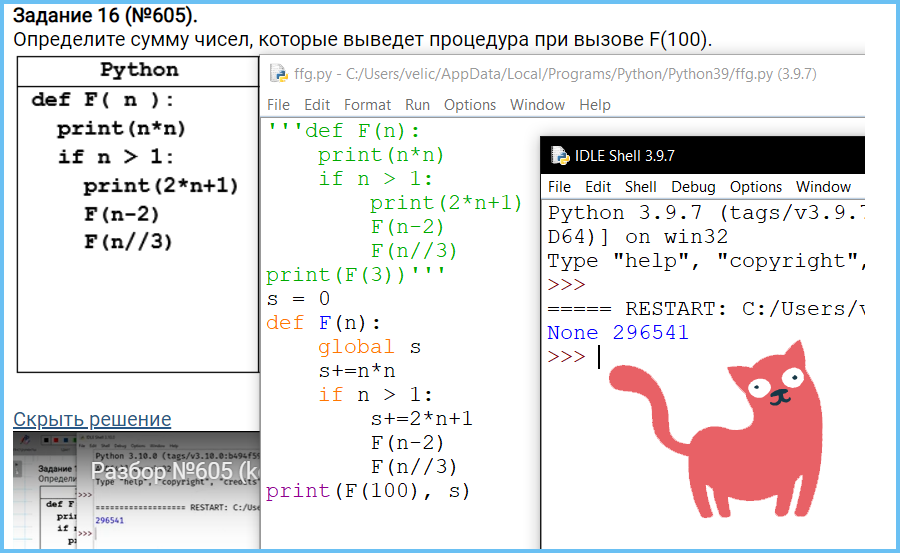
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Поляков ЕГЭ)
(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n!, если n ≥ 5000,
F(n) = 2 · F(n + 1) / (n + 1), если 1 ≤ n < 5000.
Чему равно значение выражения 1000 · F(7) / F(4)? Примечание.
Факториал числа n, который обозначается как n!, вычисляется по формуле n!=1·2·…·n.

Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для проведения вычислений с вещественными числами (числами с плавающей точкой). Для использования этих функций в начале программы необходимо подключить модуль, что делается командой import:
# программный код
import math
num1 = math.sqrt(2) # вычисление корня квадратного из двух
Как можно заметить из примера выше, для вызова функции мы вынуждены указывать название модуля и символ точки. С другой стороны, если функции используются достаточно часто, то такой вызов (постоянное указание названия модуля и символа точки) может усложнить программу и сделать её менее читабельной. Для того, чтобы не указывать название модуля и символ точки при вызове функций, мы пишем следующий код:

# программный код
from math import *
Если нужно использовать только некоторые функции модуля, то мы можем импортировать только их следующим образом: from math import sqrt, ceil, factorial

ещё не решила)