8. Перебор слов и системы счисления

Училка
28.01.2022

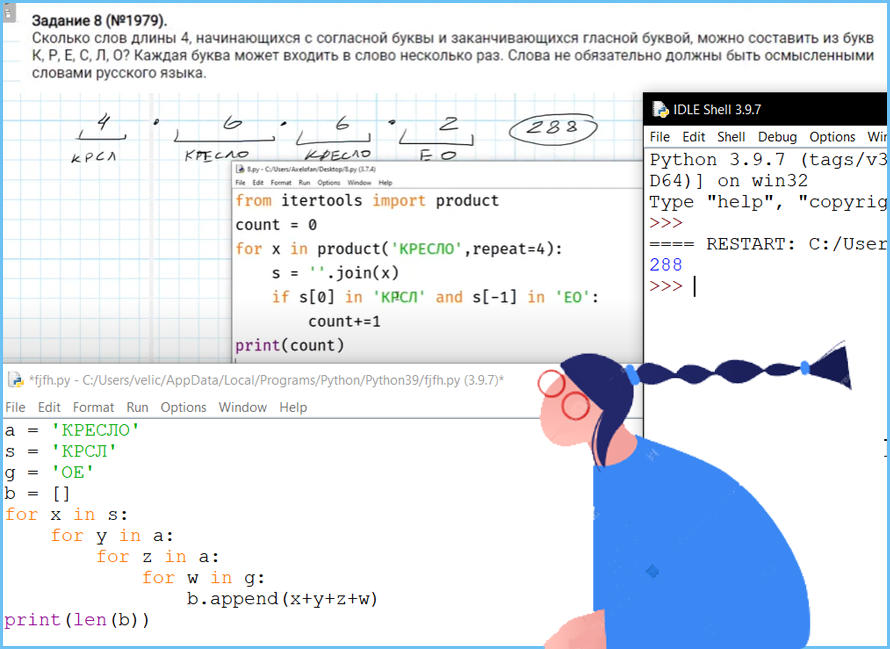
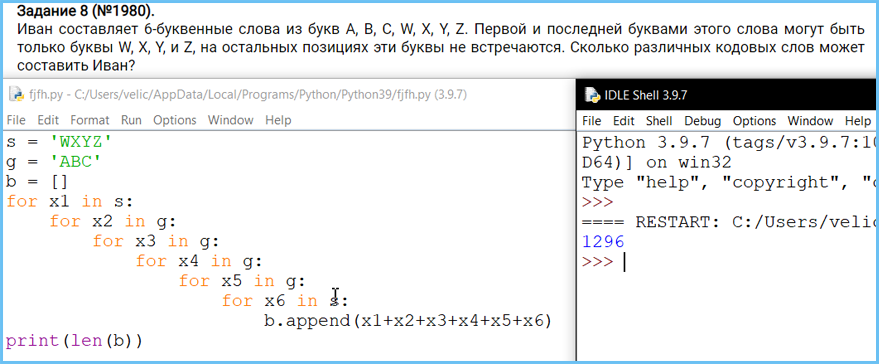
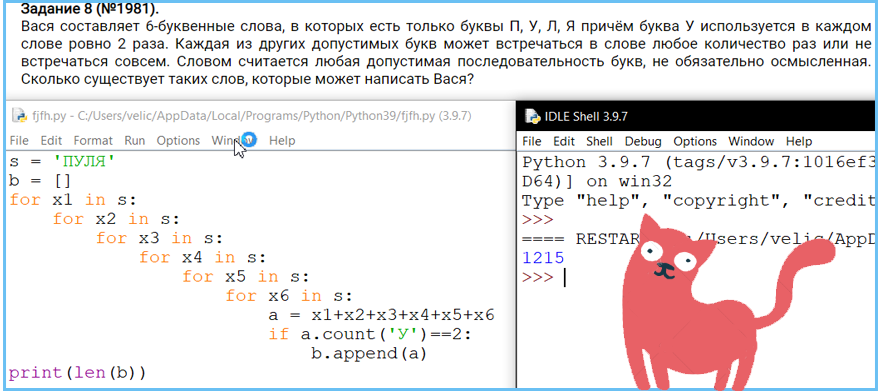
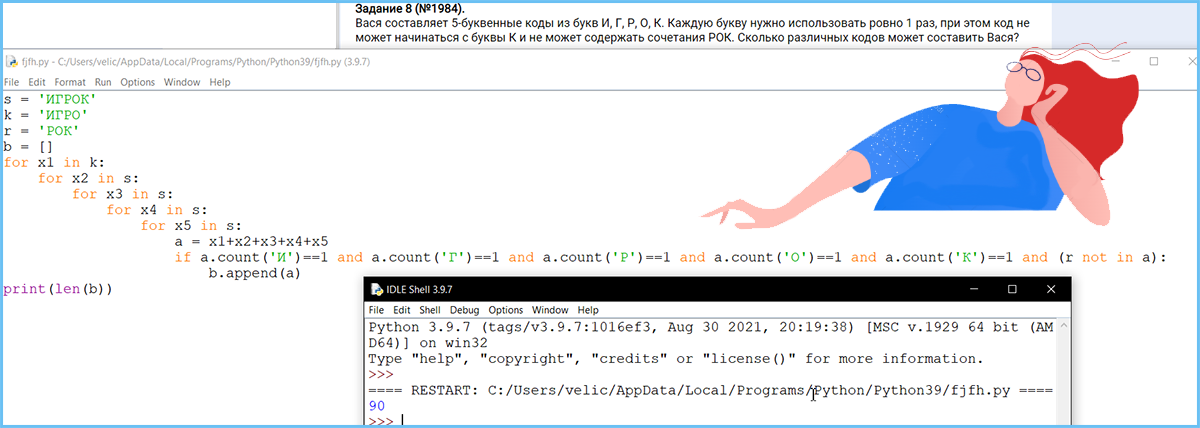
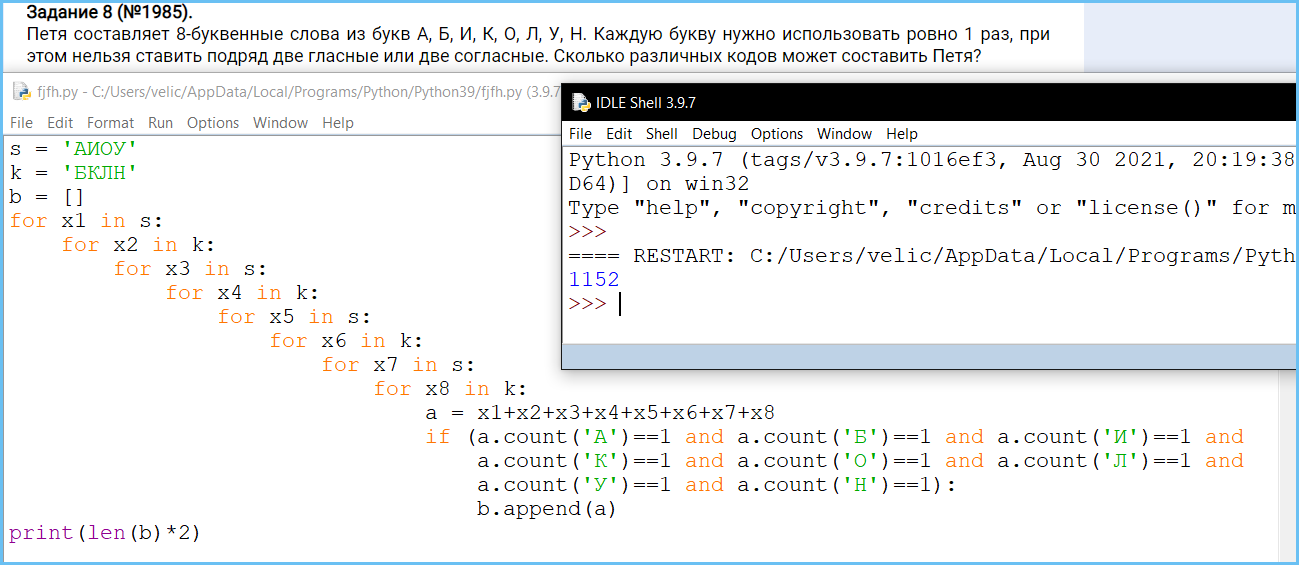
Задание 8. Кодирование данных, комбинаторика, системы счисления. Знание о методах измерения количества информации. Принципы работы с числами, записанными в позиционных системах счисления.

Решении с помощью программы на языке Python.

Комбинаторика:

Комбинаторика – это раздел математики, в котором изучаются вопросы выбора или расположения элементов множества в соответствии с заданными правилами. Комбинаторика рассматривает конечные множества.
  1. Дерево возможных вариантов. Этот метод решения комбинаторных задач помогает решать разнообразные задачи, касающиеся перебора вариантов происходящих событий.
  2. Закон умножения. Применяется, когда не требуется перечислять все возможные варианты, а нужно ответить на вопрос — сколько их существует.
  3. Закон сложения. Используется тогда, когда нужно выбрать только один элемент.
  4. Перестановки –  это специальный случай размещений, когда выборка так же велика, как данное множество.
  5. Размещениями называют комбинации, в которых имеет значение порядок элементов.
  6. Сочетаниями называют комбинации, при составлении которых важно знать только то, какие элементы выбраны, но их порядок не имеет значения.
    • В русском языке 33 буквы: 10 гласных букв (а, у, о, ы, и, э, я, ю, ё, е), 21 согласная буква (б, в, г, д, ж, з, й, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ) и два знака (ь, ъ).
    • Алфавит английского языка по написанию совпадает с латинским алфавитом и состоит из 26 букв.
ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ

ПРИМЕР:

«Игорь составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Игорь использует

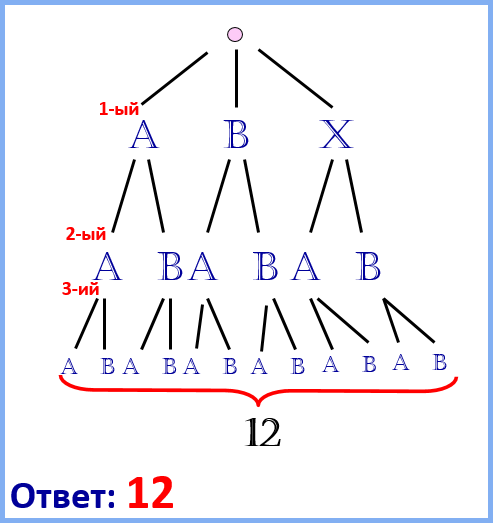
3-буквенные слова, в которых есть только буквы A, B, X, причём буква X появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Игорь?»

  1. Определить длину слова (количество уровней
    дерева).
  2. Посмотреть сколько букв может быть на
    каждом уровне.
  3. Посчитать сколько получилось слов в итоге.

Каждый путь по этому “дереву” соответствует одному из способов выбора.

Число способов выбора равно числу точек в нижнем ряду “ дерева”.

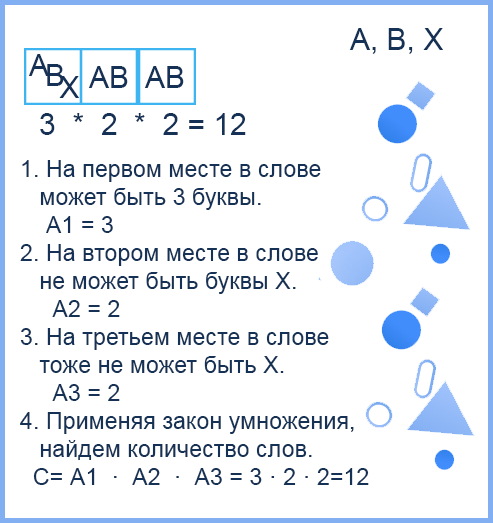
ЗАКОН УМНОЖЕНИЯ
Закон умножения – когда требуется выбрать несколько предметов из одного набора, и несколько – из другого, причем эти наборы независимы, то соответствующие сочетания просто умножаются друг на друга. получилось слов в итоге. Другими словами, пусть имеется A способов выполнить одно действие и B способов выполнить другое действие.
Путь также эти действия независимы, т.е. никак не связаны между собой. Тогда можно найти число способов выполнить первое и второе действие по формуле: C = A · B Закон умножения – это логическое «И», при котором нас интересует одновременное выполнение и первого, и второго действия.
ЗАКОН СЛОЖЕНИЯ

Закон сложения показывает, сколькими способами

   можно выполнить сложное действие, которое состоит из

   двух и более простых — при условии, что все они,

   никогда не случаются одновременно.

Чтобы использовать закон сложения:

  1. нужно понять, каковы группы, из которых нужно выбрать 1 элемент;
  2. нужно выяснить количество элементов в каждой группе;
  3. нужно убедиться, что в различных группах, из которых выбирают элемент, нет одинаковых
    элементов.

Пример:        

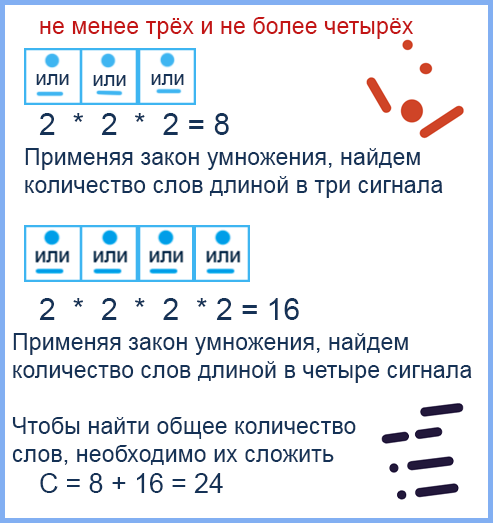
Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код азбуки Морзе длиной не менее трёх и не более четырёх сигналов (точек и тире)?

Можно сказать, что закон сложения — это логическое «ИЛИ» в комбинаторике, когда нас устраивает любой из взаимоисключающих вариантов.
ПЕРЕСТАНОВКИ
Перестановкой называется множество из n элементов, записанных в определённом порядке. Теорема о перестановках элементов конечного множества: n различных элементов можно расставить по одному на n  различных мест ровно n! способами. С = n!
Вычисляя перестановки, определяется, сколькими различными способами можно переупорядочить элементы множества, не меняя их количество.

Пример:        

Вася составляет 5-буквенные слова

из пяти буквенного алфавита (A, В, С, Д, Х). Каждая из допустимых букв может встречаться в слове только один раз. Словом, считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

Произведение подряд идущих первых n натуральных чисел обозначают n! и называют факториалом числа n.

0! = 1

1! = 1

2! = 1 · 2 = 2

3! = 1 · 2 · 3 = 6

4! = 1 · 2 · 3 · 4 = 24

n! = 1 · 2 · 3 · … · (n-1) · n

ПЕРЕСТАНОВКИ С ПОВТОРЕНИЯМИ
Перестановкой с повторением из n элементов    k типов (k ≤ n) называются все возможные последовательности исходных n элементов. Если в основном множестве k элементов a1, a2, … ak и выборка n элементов составляется так: элемент a1 повторяется n1 раз, элемент a2 повторяется n2 раз, … элемент ak повторяется nk раз, такие выборки называются перестановками с повторениями. Их возможное количество вычисляется вычисляется по формуле: C = n! / n1!*n2!..nk!
Вычисляя перестановки с повторениями, определяется, сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов

ПРИМЕР: Саша составляет слова, переставляя буквы из слова «ИДИЛЛИЯ». Словом, считается любая допустимая последовательность букв, не обязательно осмысленная.

Сколько существует различных слов, которые может написать Саша?

РАЗМЕЩЕНИЯ
Размещением из n элементов по m элементов (m≤n) называется упорядоченная выборка элементов m из данного множества элементов n. При этом:
  1. Любой элемент может оказаться на любом из m мест, но использоваться может в выборке только один раз.
  2. Порядок элементов в выборке важен.
Формула для определения числа размещений без повторений: C = n! / (n — m) !
где m показывает количество элементов размещения (сколько элементов выбирается), n показывает количество элементов данного множества.

Пример:        

Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности? 

РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ
Размещениями с повторениями называются упорядоченные выборки, содержащие m элементов из данных k элементов, причем каждый элемент исходной совокупности может участвовать в размещении несколько раз.
При этом:
  1. Допускается, что m>k.
  2. Любой элемент может оказаться на любом из m мест, и использоваться в выборке может несколько раз или не использоваться совсем.
  3. Порядок элементов в выборке важен.
Формула для расчета количества размещений с повторениями: C = km
Каждое размещение с повторениями из k элементов по m элементов может состоять не только из различных элементов, но и m каких угодно и как угодно повторяющихся элементов.
Пример: Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность важна). Какое количество различных сигналов может передать корабль при помощи четырех сигнальных флагов, если на корабле имеются флаги трех различных видов (флагов каждого вида неограниченное количество)?
СОЧЕТАНИЯ
Сочетания не являются упорядоченными наборами.
Сочетаниями без повторений называются неупорядоченные наборы, содержащие m различных элементов из данных n элементов.
   При этом:
  1. «неупорядоченные наборы», т.е. наборы AB и ВА – это одно и тоже сочетание.
  2. Любой элемент может оказаться на любом из m мест, но использоваться может в наборе только один раз.
  3. Порядок элементов в выборке не важен.
Формула для определения числа сочетаний без повторений: C = n! / (m!(n — m)!)

Пример:        

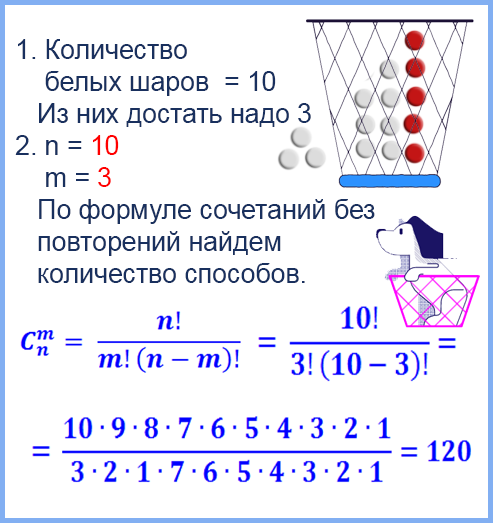
В урне 10 белых шаров и 5 черных.

Сколькими способами можно вынуть наугад 3 белых шара?

СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ
Сочетаниями с повторениями называются неупорядоченные выборки, содержащие m  элементов из данных k элементов, причем каждый элемент исходной совокупности может участвовать в сочетании несколько раз.
При этом:
  1. Наборы AB и ВА – это одно и тоже сочетание.
  2. Любой элемент может оказаться на любом из m мест, и использоваться может в наборе несколько раз.
  3. Порядок элементов в выборке не важен.
Формула для расчета количества сочетаний с повторениями:
C = (k + m — 1)! / (m!(k-1)!)

Пример:        

Сколько существует треугольников, длины сторон которых принимают одно из значений 4, 5, 6, 7

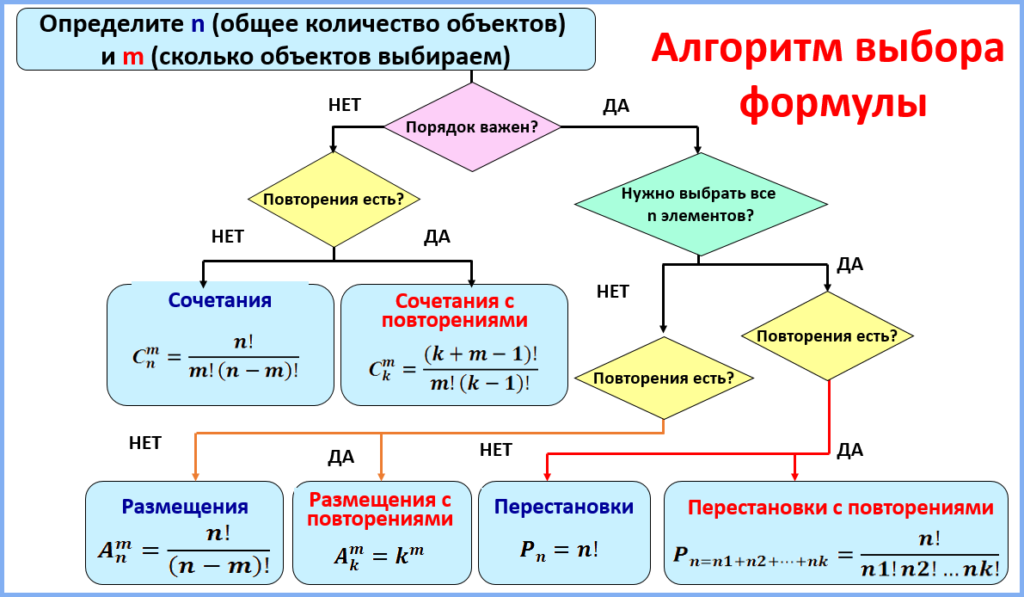
Перебор слов и системы счисления:

Для того, чтобы определить какое слово стоит под номером M от начала списка в задачах, касающихся перебора вариантов происходящих событий, необходимо:
  1. Заменить буквы цифрами, начиная с 0.
  2. Записать слова в виде чисел в системе счисления N, равной количеству букв.
  3. Порядковый номер, написанный рядом с пунктом, всегда на единицу больше, располагающегося рядом числа в N-ричной системе счисления. Поэтому уменьшаем номер слова на единицу (M-1).
  4. Переводим число (М-1) из десятичной системы счисления в систему счисления с основанием N.
  5. Заменяем полученную последовательность цифр соответствующими буквами.

Пример 1:

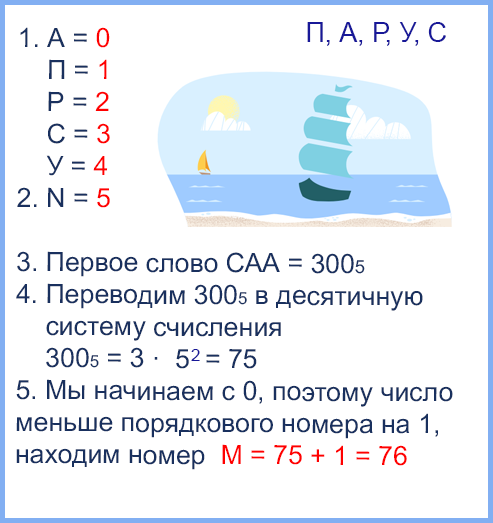
Все трёхбуквенные слова, составленные из букв П, А, Р, У, С, записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:

  1. ААА
  2. ААП
  3. ААР
  4. ААС
  5. ААУ
  6. АПА
  7. ….

Под каким номером в списке идёт первое слово, которое начинается с буквы С?

Пример 2:

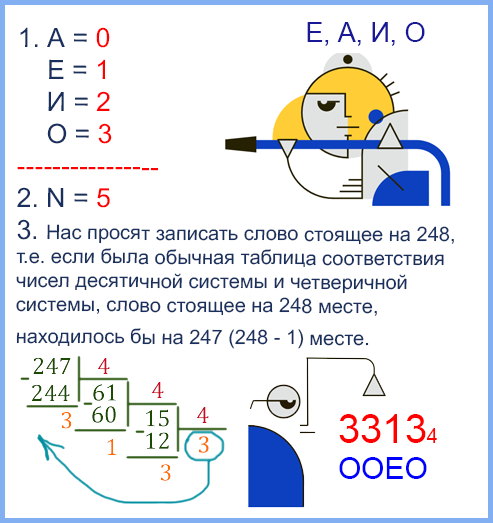
Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…

Запишите слово, стоящее на 248-м месте от начала списка.

Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.

Количество информации:

Количество информации в сообщении о некотором событии зависит от его вероятности. Чем меньше вероятность события, тем больше информации оно несёт.

Варианты решения заданий из КЕГЭ

Метки: , , ,